Functions¶
Forward substitution
1 2 3 4 5 6 7 8 9 10 11 12 13def forwardsub(L,b): """ forwardsub(L,b) Solve the lower-triangular linear system with matrix L and right-hand side vector b. """ n = len(b) x = np.zeros(n) for i in range(n): s = L[i,:i] @ x[:i] x[i] = ( b[i] - s ) / L[i, i] return x
Backward substitution
1 2 3 4 5 6 7 8 9 10 11 12 13def backsub(U,b): """ backsub(U,b) Solve the upper-triangular linear system with matrix U and right-hand side vector b. """ n = len(b) x = np.zeros(n) for i in range(n-1, -1, -1): s = U[i, i+1:] @ x[i+1:] x[i] = ( b[i] - s ) / U[i, i] return x
LU factorization (not stable)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19def lufact(A): """ lufact(A) Compute the LU factorization of square matrix A, returning the factors. """ n = A.shape[0] # detect the dimensions from the input L = np.eye(n) # ones on main diagonal, np.zeros elsewhere U = np.zeros((n, n)) A_k = np.copy(A) # make a working np.copy # Reduction by np.outer products for k in range(n-1): U[k, :] = A_k[k, :] L[:, k] = A_k[:, k] / U[k,k] A_k -= np.outer(L[:,k], U[k,:]) U[n-1, n-1] = A_k[n-1, n-1] return L, U
About the code
Line 11 of Function 2.4.1 points out a subtle issue. Array variables are really just references to blocks of memory. Such a reference is much more efficient to pass around than the complete contents of the array. However, it means that a statement A_k = A would just clone the array reference of A into the new variable. Any changes made to entries of A_k would then also be made to entries of A, because they refer to the same location in memory. In this context, we don’t want to change the original matrix, so we use copy here to create an independent copy of the array contents and a new reference to them.
LU factorization with partial pivoting
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21def plufact(A): """ plufact(A) Compute the PLU factorization of square matrix A, returning the triangular factors and a row permutation vector. """ n = A.shape[0] L = np.zeros((n, n)) U = np.zeros((n, n)) p = np.zeros(n, dtype=int) A_k = np.copy(A) # Reduction by np.outer products for k in range(n): p[k] = np.argmax(abs(A_k[:, k])) U[k, :] = A_k[p[k], :] L[:, k] = A_k[:, k] / U[k, k] if k < n-1: A_k -= np.outer(L[:, k], U[k, :]) return L[p, :], U, p
Examples¶
2.1 Polynomial interpolation¶
Example 2.1.1
We create two vectors for data about the population of China. The first has the years of census data and the other has the population, in millions of people.
year = arange(1980, 2020, 10) # from 1980 to 2020 by 10
pop = array([984.736, 1148.364, 1263.638, 1330.141])It’s convenient to measure time in years since 1980.
t = year - 1980
y = popNow we have four data points , so and we seek an interpolating cubic polynomial. We construct the associated Vandermonde matrix:
V = vander(t)
print(V)[[ 0 0 0 1]
[ 1000 100 10 1]
[ 8000 400 20 1]
[27000 900 30 1]]
To solve a linear system for the vector of polynomial coefficients, we use solve (imported from numpy.linalg):
c = linalg.solve(V, y)
print(c)[-6.95000e-05 -2.39685e-01 1.87666e+01 9.84736e+02]
The algorithms used by solve are the main topic of this chapter. As a check on the solution, we can compute the residual , which should be small (near machine precision).
Tip
Matrix multiplication in NumPy is done with @ or matmul.
print(y - V @ c)[0. 0. 0. 0.]
By our definitions, the coefficients in c are given in descending order of power in . We can use the resulting polynomial to estimate the population of China in 2005:
p = poly1d(c) # construct a polynomial
print(p(2005 - 1980)) # apply the 1980 time shift1303.0119375
The official figure was 1303.72, so our result is rather good.
We can visualize the interpolation process. First, we plot the data as points. Then we add a plot of the interpolant, taking care to shift the variable back to actual years.
scatter(year, y, color="k", label="data");
tt = linspace(0, 30, 300) # 300 times from 1980 to 2010
plot(1980 + tt, p(tt), label="interpolant");
xlabel("year");
ylabel("population (millions)");
title("Population of China");
legend();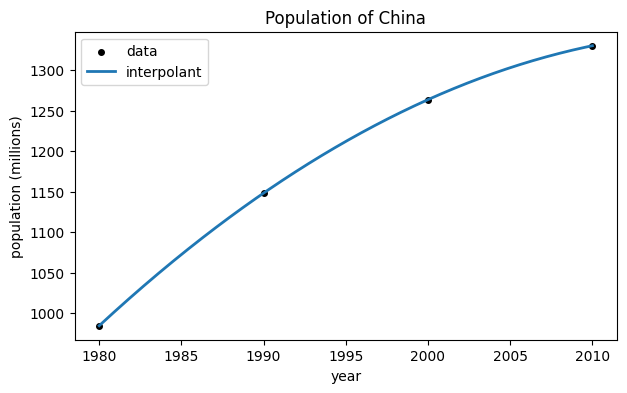
2.2 Computing with matrices¶
Example 2.2.1
A vector is created using square brackets and commas to enclose and separate its entries.
x = array([3, 3, 0, 1, 0 ])
print(x.shape)(5,)
To construct a matrix, you nest the brackets to create a “vector of vectors”. The inner vectors are the rows.
A = array([
[1, 2, 3, 4, 5],
[50, 40, 30, 20, 10],
[pi, sqrt(2), exp(1), (1+sqrt(5))/2, log(3)]
])
print(A)
print(A.shape)[[ 1. 2. 3. 4. 5. ]
[50. 40. 30. 20. 10. ]
[ 3.14159265 1.41421356 2.71828183 1.61803399 1.09861229]]
(3, 5)
In this text, we treat all vectors as equivalent to matrices with a single column. That isn’t true in NumPy, because even an array has two dimensions, unlike a vector.
array([[3], [1], [2]]).shape(3, 1)You can concatenate arrays with compatible dimensions using hstack and vstack.
print( hstack([A, A]) )[[ 1. 2. 3. 4. 5. 1.
2. 3. 4. 5. ]
[50. 40. 30. 20. 10. 50.
40. 30. 20. 10. ]
[ 3.14159265 1.41421356 2.71828183 1.61803399 1.09861229 3.14159265
1.41421356 2.71828183 1.61803399 1.09861229]]
print( vstack([A, A]) )[[ 1. 2. 3. 4. 5. ]
[50. 40. 30. 20. 10. ]
[ 3.14159265 1.41421356 2.71828183 1.61803399 1.09861229]
[ 1. 2. 3. 4. 5. ]
[50. 40. 30. 20. 10. ]
[ 3.14159265 1.41421356 2.71828183 1.61803399 1.09861229]]
Transposing a matrix is done by appending .T to it.
print(A.T)[[ 1. 50. 3.14159265]
[ 2. 40. 1.41421356]
[ 3. 30. 2.71828183]
[ 4. 20. 1.61803399]
[ 5. 10. 1.09861229]]
For matrices with complex values, we usually want instead the adjoint or hermitian, which is .conj().T.
print((x + 1j).conj().T)[3.-1.j 3.-1.j 0.-1.j 1.-1.j 0.-1.j]
There are many convenient shorthand ways of building vectors and matrices other than entering all of their entries directly or in a loop. To get a vector with evenly spaced entries between two endpoints, you have two options.
print(arange(1, 7, 2)) # from 1 to 7 (not inclusive), step by 2[1 3 5]
print(linspace(-1, 1, 5)) # from -1 to 1 (inclusive), with 5 total values[-1. -0.5 0. 0.5 1. ]
The practical difference between these is whether you want to specify the step size in arange or the number of points in linspace.
Accessing an element is done by giving one (for a vector) or two index values in square brackets. In Python, indexing always starts with zero, not 1.
A = array([
[1, 2, 3, 4, 5],
[50, 40, 30, 20, 10],
linspace(-5, 5, 5)
])
x = array([3, 2, 0, 1, -1 ])print("row 2, col 3 of A:", A[1, 2])
print("first element of x:", x[0])row 2, col 3 of A: 30.0
first element of x: 3
The indices can be ranges, in which case a slice or block of the matrix is accessed. You build these using a colon in the form start:stop. However, the last value of this range is stop-1, not stop.
print(A[1:3, 0:2]) # rows 2 and 3, cols 1 and 2[[50. 40. ]
[-5. -2.5]]
If start or stop is omitted, the range extends to the first or last index.
print(x[1:]) # elements 2 through the end[ 2 0 1 -1]
print(A[:2, 0]) # first two rows in column 1[ 1. 50.]
Notice in the last case above that even when the slice is in the shape of a column vector, the result is just a vector with one dimension and neither row nor column shape.
There are more variations on the colon ranges. A negative value means to count from the end rather than the beginning. And a colon by itself means to include everything from the relevant dimension.
print(A[:-1, :]) # all rows up to the last, all columns[[ 1. 2. 3. 4. 5.]
[50. 40. 30. 20. 10.]]
Finally, start:stop:step means to step size or stride other than one. You can mix this with the other variations.
print(x[::2]) # all the odd indexes[ 3 0 -1]
print(A[:, ::-1]) # reverse the columns[[ 5. 4. 3. 2. 1. ]
[10. 20. 30. 40. 50. ]
[ 5. 2.5 0. -2.5 -5. ]]
The matrix and vector senses of addition, subtraction, and scalar multiplication and division are all handled by the usual symbols. Two matrices of the same size (what NumPy calls shape) are operated on elementwise.
print(A - 2 * ones([3, 5])) # subtract two from each element[[-1. 0. 1. 2. 3. ]
[48. 38. 28. 18. 8. ]
[-7. -4.5 -2. 0.5 3. ]]
If one operand has a smaller number of dimensions than the other, Python tries to broadcast it in the “missing” dimension(s), and the operation proceeds if the resulting shapes are identical.
print(A - 2) # subtract two from each element[[-1. 0. 1. 2. 3. ]
[48. 38. 28. 18. 8. ]
[-7. -4.5 -2. 0.5 3. ]]
u = array([1, 2, 3, 4, 5])
print(A - u) # repeat this row for every row of A[[ 0. 0. 0. 0. 0. ]
[49. 38. 27. 16. 5. ]
[-6. -4.5 -3. -1.5 0. ]]
v = array([1, 2, 3])
print(A - v) # broadcasting this would be 3x3, so it's an error---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[29], line 2
1 v = array([1, 2, 3])
----> 2 print(A - v) # broadcasting this would be 3x3, so it's an error
ValueError: operands could not be broadcast together with shapes (3,5) (3,) print(A - v.reshape([3, 1])) # broadcasts to each column of A[[ 0. 1. 2. 3. 4. ]
[48. 38. 28. 18. 8. ]
[-8. -5.5 -3. -0.5 2. ]]
Matrix–matrix and matrix–vector products are computed using @ or matmul.
B = diag([-1, 0, -5]) # create a diagonal 3x3
print(B @ A) # matrix product[[ -1. -2. -3. -4. -5. ]
[ 0. 0. 0. 0. 0. ]
[ 25. 12.5 0. -12.5 -25. ]]
is undefined for these matrix sizes.
print(A @ B) # incompatible sizes---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[32], line 1
----> 1 print(A @ B) # incompatible sizes
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 3 is different from 5)The multiplication operator * is reserved for elementwise multiplication. Both operands have to be the same size, after any potential broadcasts.
print(B * A) # not the same size, so it's an error---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[33], line 1
----> 1 print(B * A) # not the same size, so it's an error
ValueError: operands could not be broadcast together with shapes (3,3) (3,5) print((A / 2) * A) # elementwise[[5.000e-01 2.000e+00 4.500e+00 8.000e+00 1.250e+01]
[1.250e+03 8.000e+02 4.500e+02 2.000e+02 5.000e+01]
[1.250e+01 3.125e+00 0.000e+00 3.125e+00 1.250e+01]]
To raise to a power elementwise, use a double star. This will broadcast as well.
print(B)
print(B**3)[[-1 0 0]
[ 0 0 0]
[ 0 0 -5]]
[[ -1 0 0]
[ 0 0 0]
[ 0 0 -125]]
print(x)
print(2.0**x)[ 3 2 0 1 -1]
[8. 4. 1. 2. 0.5]
Most of the mathematical functions, such as cos, sin, log, exp and sqrt, expecting scalars as operands will be broadcast to arrays.
print(cos(pi * x))[-1. 1. 1. -1. -1.]
2.3 Linear systems¶
Example 2.3.2
For a square matrix , the command solve(A, B) from numpy.linalg is mathematically equivalent to .
A = array([[1, 0, -1], [2, 2, 1], [-1, -3, 0]])
b = array([1, 2, 3])x = linalg.solve(A, b)
print(x)[ 2.14285714 -1.71428571 1.14285714]
One way to check the answer is to compute a quantity known as the residual. It is (ideally) close to machine precision(relative to the elements in the data).
residual = b - A @ x
print(residual)[-4.4408921e-16 -4.4408921e-16 0.0000000e+00]
If the matrix is singular, you may get an error.
A = array([[0, 1], [0, 0]])
b = array([1, -1])
linalg.solve(A, b) # error, singular matrix---------------------------------------------------------------------------
LinAlgError Traceback (most recent call last)
Cell In[41], line 3
1 A = array([[0, 1], [0, 0]])
2 b = array([1, -1])
----> 3 linalg.solve(A, b) # error, singular matrix
File ~/mambaforge/envs/myst/lib/python3.13/site-packages/numpy/linalg/_linalg.py:413, in solve(a, b)
410 signature = 'DD->D' if isComplexType(t) else 'dd->d'
411 with errstate(call=_raise_linalgerror_singular, invalid='call',
412 over='ignore', divide='ignore', under='ignore'):
--> 413 r = gufunc(a, b, signature=signature)
415 return wrap(r.astype(result_t, copy=False))
File ~/mambaforge/envs/myst/lib/python3.13/site-packages/numpy/linalg/_linalg.py:104, in _raise_linalgerror_singular(err, flag)
103 def _raise_linalgerror_singular(err, flag):
--> 104 raise LinAlgError("Singular matrix")
LinAlgError: Singular matrixA linear system with a singular matrix might have no solution or infinitely many solutions, but in either case, a numerical solution becomes trickier. Detecting singularity is a lot like checking whether two floating-point numbers are exactly equal: because of roundoff, it could be missed. We’re headed toward a more robust way to fully describe this situation.
Example 2.3.3
It’s easy to get just the lower triangular part of any matrix using the tril function.
A = 1 + floor(9 * random.rand(5, 5))
L = tril(A)
print(L)[[4. 0. 0. 0. 0.]
[6. 7. 0. 0. 0.]
[3. 2. 9. 0. 0.]
[3. 6. 3. 8. 0.]
[7. 9. 7. 3. 9.]]
We’ll set up and solve a linear system with this matrix.
b = ones(5)
x = FNC.forwardsub(L, b)
print(x)[ 0.25 -0.07142857 0.04365079 0.06845238 -0.06867284]
It’s not clear how accurate this answer is. However, the residual should be zero or comparable to .
b - L @ xarray([0., 0., 0., 0., 0.])Next we’ll engineer a problem to which we know the exact answer.
alpha = 0.3;
beta = 2.2;
U = diag(ones(5)) + diag([-1, -1, -1, -1], k=1)
U[0, 3:5] = [ alpha - beta, beta ]
print(U)[[ 1. -1. 0. -1.9 2.2]
[ 0. 1. -1. 0. 0. ]
[ 0. 0. 1. -1. 0. ]
[ 0. 0. 0. 1. -1. ]
[ 0. 0. 0. 0. 1. ]]
x_exact = ones(5)
b = array([alpha, 0, 0, 0, 1])
x = FNC.backsub(U, b)
print("error:", x - x_exact)error: [2.22044605e-16 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00]
Everything seems OK here. But another example, with a different value for β, is more troubling.
alpha = 0.3;
beta = 1e12;
U = diag(ones(5)) + diag([-1, -1, -1, -1], k=1)
U[0, 3:5] = [ alpha - beta, beta ]
b = array([alpha, 0, 0, 0, 1])
x = FNC.backsub(U, b)
print("error:", x - x_exact)error: [-4.8828125e-05 0.0000000e+00 0.0000000e+00 0.0000000e+00
0.0000000e+00]
It’s not so good to get 4 digits of accuracy after starting with sixteen! But the source of the error is not hard to track down. Solving for performs in the first row. Since is so much smaller than , this a recipe for losing digits to subtractive cancellation.
2.4 LU factorization¶
Example 2.4.2
We explore the outer product formula for two random triangular matrices.
from numpy.random import randint
L = tril(randint(1, 10, size=(3, 3)))
print(L)[[9 0 0]
[4 5 0]
[5 7 2]]
U = triu(randint(1, 10, size=(3, 3)))
print(U)[[9 5 5]
[0 7 1]
[0 0 1]]
Here are the three outer products appearing in the sum in (2.4.4):
print(outer(L[:, 0], U[0, :]))[[81 45 45]
[36 20 20]
[45 25 25]]
print(outer(L[:, 1], U[1, :]))[[ 0 0 0]
[ 0 35 5]
[ 0 49 7]]
print(outer(L[:, 2], U[2, :]))[[0 0 0]
[0 0 0]
[0 0 2]]
Simply because of the triangular zero structures, only the first outer product contributes to the first row and first column of the entire product.
Example 2.4.3
For illustration, we work on a matrix. We name it with a subscript in preparation for what comes.
A_1 = array([
[2, 0, 4, 3],
[-4, 5, -7, -10],
[1, 15, 2, -4.5],
[-2, 0, 2, -13]
])
L = eye(4)
U = zeros((4, 4));Now we appeal to (2.4.5). Since , we see that the first row of is just the first row of .
U[0, :] = A_1[0, :]
print(U)[[2. 0. 4. 3.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
From (2.4.6), we see that we can find the first column of from the first column of .
L[:, 0] = A_1[:, 0] / U[0, 0]
print(L)[[ 1. 0. 0. 0. ]
[-2. 1. 0. 0. ]
[ 0.5 0. 1. 0. ]
[-1. 0. 0. 1. ]]
We have obtained the first term in the sum (2.4.4) for , and we subtract it away from .
A_2 = A_1 - outer(L[:, 0], U[0, :])Now If we ignore the first row and first column of the matrices in this equation, then in what remains we are in the same situation as at the start. Specifically, only has any effect on the second row and column, so we can deduce them now.
U[1, :] = A_2[1, :]
L[:, 1] = A_2[:, 1] / U[1, 1]
print(L)[[ 1. 0. 0. 0. ]
[-2. 1. 0. 0. ]
[ 0.5 3. 1. 0. ]
[-1. 0. 0. 1. ]]
If we subtract off the latest outer product, we have a matrix that is zero in the first two rows and columns.
A_3 = A_2 - outer(L[:, 1], U[1, :])Now we can deal with the lower right submatrix of the remainder in a similar fashion.
U[2, :] = A_3[2, :]
L[:, 2] = A_3[:, 2] / U[2, 2]
A_4 = A_3 - outer(L[:, 2], U[2, :])Finally, we pick up the last unknown in the factors.
U[3, 3] = A_4[3, 3]We now have all of ,
print(L)[[ 1. 0. -0. 0. ]
[-2. 1. -0. 0. ]
[ 0.5 3. 1. 0. ]
[-1. 0. -2. 1. ]]
and all of ,
print(U)[[ 2. 0. 4. 3.]
[ 0. 5. 1. -4.]
[ 0. 0. -3. 6.]
[ 0. 0. 0. 2.]]
We can verify that we have a correct factorization of the original matrix by computing the backward error:
A_1 - L @ Uarray([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])In floating point, we cannot expect the difference to be exactly zero as we found in this toy example. Instead, we would be satisfied to see that each element of the difference above is comparable in size to machine precision.
Example 2.4.4
Here are the data for a linear system .
A = array([
[2, 0, 4, 3],
[-4, 5, -7, -10],
[1, 15, 2, -4.5],
[-2, 0, 2, -13]
])
b = array([4, 9, 9, 4])We apply Function 2.4.1 and then do two triangular solves.
L, U = FNC.lufact(A)
z = FNC.forwardsub(L, b)
x = FNC.backsub(U, z)A check on the residual assures us that we found the solution.
b - A @ xarray([0.00000000e+00, 0.00000000e+00, 2.84217094e-14, 0.00000000e+00])2.5 Efficiency of matrix computations¶
Example 2.5.4
Here is a straightforward implementation of matrix-vector multiplication.
n = 6
A = random.rand(n, n)
x = ones(n)
y = zeros(n)
for i in range(n):
for j in range(n):
y[i] += A[i, j] * x[j] # 2 flopsEach of the loops implies a summation of flops. The total flop count for this algorithm is
Since the matrix has elements, all of which have to be involved in the product, it seems unlikely that we could get a flop count that is smaller than in general.
Let’s run an experiment with the built-in matrix-vector multiplication. We assume that flops dominate the computation time and thus measure elapsed time.
N = 400 * arange(1, 11)
t = []
print(" n t")
for i, n in enumerate(N):
A = random.randn(n, n)
x = random.randn(n)
start = timer()
for j in range(50): A @ x
t.append(timer() - start)
print(f"{n:5} {t[-1]:10.3e}") n t
400 5.891e-04
800 1.704e-03
1200 1.618e-01
1600 6.045e-02
2000 2.421e-01
2400 4.623e-01
2800 5.767e-01
3200 7.574e-01
3600 1.255e+00
4000 1.606e+00
The reason for doing multiple repetitions at each value of above is to avoid having times so short that the resolution of the timer is a factor.
Looking at the timings just for and , they have ratio:
print(t[9] / t[4])6.6317187799180655
If the run time is dominated by flops, then we expect this ratio to be
Example 2.5.5
Let’s repeat the experiment of the previous example for more, and larger, values of .
N = arange(400, 6200, 200)
t = zeros(len(N))
for i, n in enumerate(N):
A = random.randn(n,n)
x = random.randn(n)
start = timer()
for j in range(20): A@x
t[i] = timer() - startPlotting the time as a function of on log-log scales is equivalent to plotting the logs of the variables, but is formatted more neatly.
fig, ax = subplots()
ax.loglog(N, t, "-o", label="observed")
ylabel("elapsed time (sec)");
xlabel("$n$");
title("Timing of matrix-vector multiplications");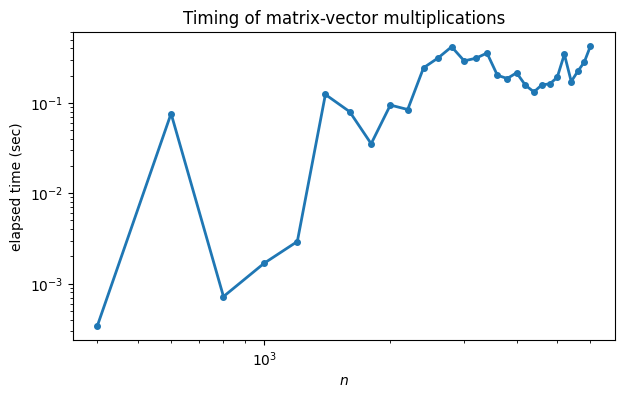
You can see that while the full story is complicated, the graph is trending to a straight line of positive slope. For comparison, we can plot a line that represents growth exactly. (All such lines have slope equal to 2.)
ax.loglog(N, t[-1] * (N/N[-1])**2, "--", label="$O(n^2)$")
ax.legend(); fig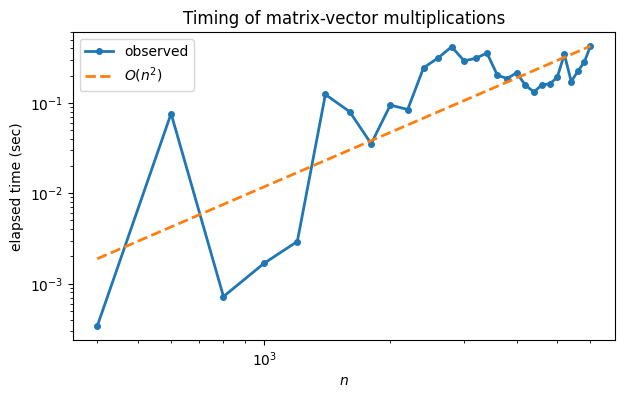
Example 2.5.6
We’ll test the conclusion of flops experimentally using the lu function imported from scipi.linalg.
from scipy.linalg import lu
N = arange(200, 2600, 200)
t = zeros(len(N))
for i, n in enumerate(N):
A = random.randn(n,n)
start = timer()
for j in range(5): lu(A)
t[i] = timer() - startWe plot the timings on a log-log graph and compare it to . The result could vary significantly from machine to machine, but in theory the data should start to parallel the line as .
loglog(N, t, "-o", label="obseved")
loglog(N, t[-1] * (N / N[-1])**3, "--", label="$O(n^3)$")
legend();
xlabel("$n$");
ylabel("elapsed time (sec)");
title("Timing of LU factorizations");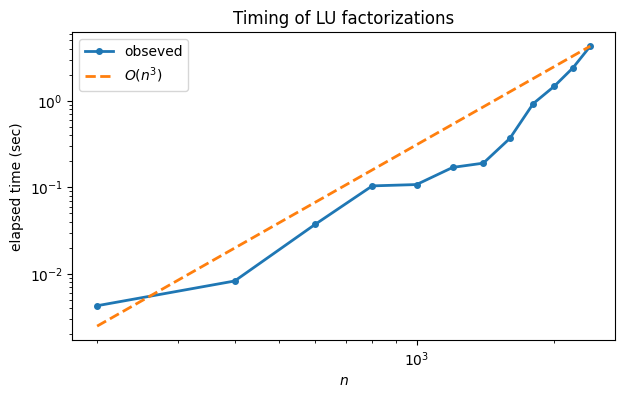
2.6 Row pivoting¶
Example 2.6.1
Here is a previously encountered matrix that factors well.
A = array([
[2, 0, 4, 3],
[-4, 5, -7, -10],
[1, 15, 2, -4.5],
[-2, 0, 2, -13]
])
L, U = FNC.lufact(A)
print(L)[[ 1. 0. -0. 0. ]
[-2. 1. -0. 0. ]
[ 0.5 3. 1. 0. ]
[-1. 0. -2. 1. ]]
If we swap the second and fourth rows of , the result is still nonsingular. However, the factorization now fails.
A[[1, 3], :] = A[[3, 1], :]
L, U = FNC.lufact(A)
print(L)[[ 1. nan nan 0. ]
[-1. nan nan 0. ]
[ 0.5 inf nan 0. ]
[-2. inf nan 1. ]]
/Users/driscoll/Dropbox/Mac/Documents/GitHub/fnc/python/fncbook/fncbook/chapter02.py:47: RuntimeWarning: divide by zero encountered in divide
L[:, k] = A_k[:, k] / U[k,k]
/Users/driscoll/Dropbox/Mac/Documents/GitHub/fnc/python/fncbook/fncbook/chapter02.py:47: RuntimeWarning: invalid value encountered in divide
L[:, k] = A_k[:, k] / U[k,k]
/Users/driscoll/mambaforge/envs/myst/lib/python3.13/site-packages/numpy/_core/numeric.py:983: RuntimeWarning: invalid value encountered in multiply
return multiply(a.ravel()[:, newaxis], b.ravel()[newaxis, :], out)
The presence of NaN in the result indicates that some impossible operation was required. The source of the problem is easy to locate. We can find the first outer product in the factorization just fine:
U[0, :] = A[0, :]
L[:, 0] = A[:, 0] / U[0, 0]
A -= outer(L[:, 0], U[0, :])
print(A)[[ 0. 0. 0. 0.]
[ 0. 0. 6. -10.]
[ 0. 15. 0. -6.]
[ 0. 5. 1. -4.]]
The next step is U[1, :] = A[1, :], which is also OK. But then we are supposed to divide by U[1, 1], which is zero. The algorithm cannot continue.
Example 2.6.2
Here is the trouble-making matrix from Demo 2.6.1.
A_1 = array([
[2, 0, 4, 3],
[-2, 0, 2, -13],
[1, 15, 2, -4.5],
[-4, 5, -7, -10]
])We now find the largest candidate pivot in the first column. We don’t care about sign, so we take absolute values before finding the max.
Tip
The argmax function returns the location of the largest element of a vector or matrix.
i = argmax( abs(A_1[:, 0]) )
print(i)3
This is the row of the matrix that we extract to put into . That guarantees that the division used to find will be valid.
L, U = eye(4), zeros((4, 4))
U[0, :] = A_1[i, :]
L[:, 0] = A_1[:, 0] / U[0, 0]
A_2 = A_1 - outer(L[:, 0], U[0, :])
print(A_2)[[ 0. 2.5 0.5 -2. ]
[ 0. -2.5 5.5 -8. ]
[ 0. 16.25 0.25 -7. ]
[ 0. 0. 0. 0. ]]
Observe that has a new zero row and zero column, but the zero row is the fourth rather than the first. However, we forge on by using the largest possible pivot in column 2 for the next outer product.
i = argmax( abs(A_2[:, 1]) )
print(f"new pivot row is {i}")
U[1, :] = A_2[i, :]
L[:, 1] = A_2[:, 1] / U[1, 1]
A_3 = A_2 - outer(L[:, 1], U[1, :])
print(A_3)new pivot row is 2
[[ 0. 0. 0.46153846 -0.92307692]
[ 0. 0. 5.53846154 -9.07692308]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
Now we have zeroed out the third row as well as the second column. We can finish out the procedure.
i = argmax( abs(A_3[:, 2]) )
print(f"new pivot row is {i}")
U[2, :] = A_3[i, :]
L[:, 2] = A_3[:, 2] / U[2, 2]
A_4 = A_3 - outer(L[:, 2], U[2, :])
print(A_4)new pivot row is 1
[[ 0. 0. 0. -0.16666667]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
i = argmax( abs(A_4[:, 3]) )
print(f"new pivot row is {i}")
U[3, :] = A_4[i, :]
L[:, 3] = A_4[:, 3] / U[3, 3];new pivot row is 0
We do have a factorization of the original matrix:
A_1 - L @ Uarray([[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00]])And has the required structure:
print(U)[[ -4. 5. -7. -10. ]
[ 0. 16.25 0.25 -7. ]
[ 0. 0. 5.53846154 -9.07692308]
[ 0. 0. 0. -0.16666667]]
However, the triangularity of has been broken.
print(L)[[-0.5 0.15384615 0.08333333 1. ]
[ 0.5 -0.15384615 1. -0. ]
[-0.25 1. 0. -0. ]
[ 1. 0. 0. -0. ]]
Example 2.6.3
Here again is the matrix from Demo 2.6.2.
A = array([
[2, 0, 4, 3],
[-2, 0, 2, -13],
[1, 15, 2, -4.5],
[-4, 5, -7, -10]
])As the factorization proceeded, the pivots were selected from rows 4, 3, 2, and finally 1 (with NumPy indices being one less). If we were to put the rows of into that order, then the algorithm would run exactly like the plain LU factorization from LU factorization.
B = A[[3, 2, 1, 0], :]
L, U = FNC.lufact(B);We obtain the same as before:
print(U)[[ -4. 5. -7. -10. ]
[ 0. 16.25 0.25 -7. ]
[ 0. 0. 5.53846154 -9.07692308]
[ 0. 0. 0. -0.16666667]]
And has the same rows as before, but arranged into triangular order:
print(L)[[ 1. 0. 0. 0. ]
[-0.25 1. 0. 0. ]
[ 0.5 -0.15384615 1. 0. ]
[-0.5 0.15384615 0.08333333 1. ]]
Example 2.6.4
The third output of plufact is the permutation vector we need to apply to .
A = random.randn(4, 4)
L, U, p = FNC.plufact(A)
A[p, :] - L @ U # should be ≈ 0array([[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, -1.11022302e-16,
5.55111512e-17],
[ 0.00000000e+00, 1.11022302e-16, 0.00000000e+00,
2.22044605e-16]])Given a vector , we solve by first permuting the entries of and then proceeding as before.
b = random.randn(4)
z = FNC.forwardsub(L, b[p])
x = FNC.backsub(U, z)A residual check is successful:
b - A @ xarray([ 0.00000000e+00, 0.00000000e+00, -2.22044605e-16, -1.11022302e-16])Example 2.6.5
In linalg.solve, the matrix A is PLU-factored, followed by two triangular solves. If we want to do those steps seamlessly, we can use the lu_factor and lu_solve from scipy.linalg.
from scipy.linalg import lu_factor, lu_solve
A = random.randn(500, 500)
b = ones(500)
LU, perm = lu_factor(A)
x = lu_solve((LU, perm), b)Why would we ever bother with this? In Efficiency of matrix computations we showed that the factorization is by far the most costly part of the solution process. A factorization object allows us to do that costly step only once per matrix, but solve with multiple right-hand sides.
start = timer()
for k in range(50): linalg.solve(A, random.rand(500))
print(f"elapsed time for 50 full solves: {timer() - start}")
start = timer()
LU, perm = lu_factor(A)
for k in range(50): lu_solve((LU, perm), random.rand(500))
print(f"elapsed time for 50 shortcut solves: {timer() - start}")elapsed time for 50 full solves: 0.760492041001271
elapsed time for 50 shortcut solves: 0.019780083999648923
Example 2.6.6
We construct a linear system for this matrix with and exact solution :
ep = 1e-12
A = array([[-ep, 1], [1, -1]])
b = A @ array([1, 1])We can factor the matrix without pivoting and solve for .
L, U = FNC.lufact(A)
print(FNC.backsub( U, FNC.forwardsub(L, b) ))[0.99997788 1. ]
Note that we have obtained only about 5 accurate digits for . We could make the result even more inaccurate by making ε even smaller:
ep = 1e-20;
A = array([[-ep, 1], [1, -1]])
b = A @ array([1, 1])
L, U = FNC.lufact(A)
print(FNC.backsub( U, FNC.forwardsub(L, b) ))[-0. 1.]
This effect is not due to ill conditioning of the problem—a solution with PLU factorization works perfectly:
print(linalg.solve(A, b))[1. 1.]
2.7 Vector and matrix norms¶
Example 2.7.1
The norm function from numpy.linalg computes vector norms.
from numpy.linalg import norm
x = array([2, -3, 1, -1])
print(norm(x)) # 2-norm by default3.872983346207417
print(norm(x, inf))3.0
print(norm(x, 1))7.0
Example 2.7.2
from numpy.linalg import norm
A = array([ [2, 0], [1, -1] ])The default matrix norm is not the 2-norm. Instead, you must provide the 2 explicitly.
print(norm(A, 2))2.2882456112707374
You can get the 1-norm as well.
print(norm(A, 1))3.0
The 1-norm is equivalent to
print(max( sum(abs(A), axis=0)) ) # sum down the rows3
Similarly, we can get the ∞-norm and check our formula for it.
print(norm(A, inf))2.0
print(max( sum(abs(A), axis=1)) ) # sum across columns2
Here we illustrate the geometric interpretation of the 2-norm. First, we will sample a lot of vectors on the unit circle in .
theta = linspace(0, 2*pi, 601)
x = vstack([cos(theta), sin(theta)]) # 601 unit columnsThe linear function defines a mapping from to . We can apply A to every column of x simply by using a matrix multiplication.
y = A @ xWe plot the unit circle on the left and the image of all mapped vectors on the right:
subplot(1,2,1)
plot(x[0, :], x[1, :])
axis("equal")
title("Unit circle")
xlabel("$x_1$")
ylabel("$x_2$")
subplot(1,2,2)
plot(y[0, :], y[1, :])
plot(norm(A, 2) * x[0, :], norm(A,2) * x[1, :],"--")
axis("equal")
title("Image under map")
xlabel("$y_1$")
ylabel("$y_2$");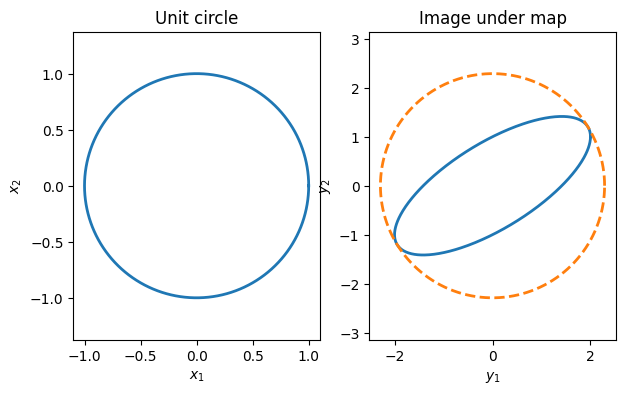
As seen on the right-side plot, the image of the transformed vectors is an ellipse that just touches the circle of radius .
2.8 Conditioning of linear systems¶
Example 2.8.1
The function cond from numpy.linalg is used to computes matrix condition numbers. By default, the 2-norm is used. As an example, the family of Hilbert matrices is famously badly conditioned. Here is the case.
A = array([
[1/(i + j + 2) for j in range(6)]
for i in range(6)
])
print(A)[[0.5 0.33333333 0.25 0.2 0.16666667 0.14285714]
[0.33333333 0.25 0.2 0.16666667 0.14285714 0.125 ]
[0.25 0.2 0.16666667 0.14285714 0.125 0.11111111]
[0.2 0.16666667 0.14285714 0.125 0.11111111 0.1 ]
[0.16666667 0.14285714 0.125 0.11111111 0.1 0.09090909]
[0.14285714 0.125 0.11111111 0.1 0.09090909 0.08333333]]
from numpy.linalg import cond
kappa = cond(A)
print(f"kappa is {kappa:.3e}")kappa is 5.110e+07
Next we engineer a linear system problem to which we know the exact answer.
x_exact = 1.0 + arange(6)
b = A @ x_exactNow we perturb the data randomly with a vector of norm 10-12.
dA = random.randn(6, 6)
dA = 1e-12 * (dA / norm(dA, 2))
db = random.randn(6)
db = 1e-12 * (db / norm(db, 2))We solve the perturbed problem using built-in pivoted LU and see how the solution was changed.
x = linalg.solve(A + dA, b + db)
dx = x - x_exactHere is the relative error in the solution.
print(f"relative error is {norm(dx) / norm(x_exact):.2e}")relative error is 2.56e-06
And here are upper bounds predicted using the condition number of the original matrix.
print(f"b_bound: {kappa * 1e-12 / norm(b):.2e}")
print(f"A_bound: {kappa * 1e-12 / norm(A, 2):.2e}")b_bound: 6.72e-06
A_bound: 4.57e-05
Even if we don’t make any manual perturbations to the data, machine epsilon does when we solve the linear system numerically.
x = linalg.solve(A, b)
print(f"relative error: {norm(x - x_exact) / norm(x_exact):.2e}")
print(f"rounding bound: {kappa / 2**52:.2e}")relative error: 6.85e-10
rounding bound: 1.13e-08
Because , it’s possible to lose 8 digits of accuracy in the process of passing from and to . That’s independent of the algorithm; it’s inevitable once the data are expressed in double precision.
Larger Hilbert matrices are even more poorly conditioned.
A = array([ [1/(i+j+2) for j in range(14)] for i in range(14) ])
kappa = cond(A)
print(f"kappa is {kappa:.3e}")kappa is 1.436e+19
Before we compute the solution, note that κ exceeds 1/eps. In principle we therefore might end up with an answer that is completely wrong (i.e., a relative error greater than 100%).
print(f"rounding bound: {kappa / 2**52:.2e}")rounding bound: 3.19e+03
x_exact = 1.0 + arange(14)
b = A @ x_exact
x = linalg.solve(A, b)We got an answer. But in fact, the error does exceed 100%:
print(f"relative error: {norm(x - x_exact) / norm(x_exact):.2e}")relative error: 1.42e+01
2.9 Exploiting matrix structure¶
Example 2.9.1
Here is a matrix with both lower and upper bandwidth equal to one. Such a matrix is called tridiagonal.
A = array([
[2, -1, 0, 0, 0, 0],
[4, 2, -1, 0, 0, 0],
[0, 3, 0, -1, 0, 0],
[0, 0, 2, 2, -1, 0],
[0, 0, 0, 1, 1, -1],
[0, 0, 0, 0, 0, 2 ]
])We can extract the elements on any diagonal using the diag command. The “main” or central diagonal is numbered zero, above and to the right of that is positive, and below and to the left is negative.
print( diag(A) )[2 2 0 2 1 2]
print( diag(A, 1) )[-1 -1 -1 -1 -1]
print( diag(A, -1) )[4 3 2 1 0]
We can also construct matrices by specifying a diagonal with the diag function.
A = A + diag([pi, 8, 6, 7], 2)
print(A)[[ 2. -1. 3.14159265 0. 0. 0. ]
[ 4. 2. -1. 8. 0. 0. ]
[ 0. 3. 0. -1. 6. 0. ]
[ 0. 0. 2. 2. -1. 7. ]
[ 0. 0. 0. 1. 1. -1. ]
[ 0. 0. 0. 0. 0. 2. ]]
L, U = FNC.lufact(A)
print(L)[[1. 0. 0. 0. 0. 0. ]
[2. 1. 0. 0. 0. 0. ]
[0. 0.75 1. 0. 0. 0. ]
[0. 0. 0.36614016 1. 0. 0. ]
[0. 0. 0. 0.21915497 1. 0. ]
[0. 0. 0. 0. 0. 1. ]]
print(U)[[ 2. -1. 3.14159265 0. 0. 0. ]
[ 0. 4. -7.28318531 8. 0. 0. ]
[ 0. 0. 5.46238898 -7. 6. 0. ]
[ 0. 0. 0. 4.56298115 -3.19684099 7. ]
[ 0. 0. 0. 0. 1.70060359 -2.53408479]
[ 0. 0. 0. 0. 0. 2. ]]
Observe above that the lower and upper bandwidths of are preserved in the factor matrices.
Example 2.9.2
We begin with a symmetric .
A_1 = array([
[2, 4, 4, 2],
[4, 5, 8, -5],
[4, 8, 6, 2],
[2, -5, 2, -26]
])We won’t use pivoting, so the pivot element is at position (1,1). This will become the first element on the diagonal of . Then we divide by that pivot to get the first column of .
L = eye(4)
d = zeros(4)
d[0] = A_1[0, 0]
L[:, 0] = A_1[:, 0] / d[0]
A_2 = A_1 - d[0] * outer(L[:, 0], L[:, 0])
print(A_2)[[ 0. 0. 0. 0.]
[ 0. -3. 0. -9.]
[ 0. 0. -2. -2.]
[ 0. -9. -2. -28.]]
We are now set up the same way for the submatrix in rows and columns 2–4.
d[1] = A_2[1, 1]
L[:, 1] = A_2[:, 1] / d[1]
A_3 = A_2 - d[1] * outer(L[:, 1], L[:, 1])
print(A_3)[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. -2. -2.]
[ 0. 0. -2. -1.]]
We continue working our way down the diagonal.
d[2] = A_3[2, 2]
L[:, 2] = A_3[:, 2] / d[2]
A_4 = A_3 - d[2] * outer(L[:, 2], L[:, 2])
print(A_4)[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 1.]]
We have arrived at the desired factorization.
d[3] = A_4[3, 3]
print("diagonal of D:")
print(d)
print("L:")
print(L)diagonal of D:
[ 2. -3. -2. 1.]
L:
[[ 1. -0. -0. 0.]
[ 2. 1. -0. 0.]
[ 2. -0. 1. 0.]
[ 1. 3. 1. 1.]]
This should be comparable to machine roundoff:
print(norm(A_1 - (L @ diag(d) @ L.T), 2) / norm(A_1))0.0
Example 2.9.3
A randomly chosen matrix is extremely unlikely to be symmetric. However, there is a simple way to symmetrize one.
A = 1.0 + floor(9 * random.rand(4, 4))
B = A + A.T
print(B)[[ 8. 12. 10. 7.]
[12. 6. 12. 6.]
[10. 12. 14. 4.]
[ 7. 6. 4. 8.]]
Similarly, a random symmetric matrix is unlikely to be positive definite. The Cholesky algorithm always detects a non-PD matrix by quitting with an error.
from numpy.linalg import cholesky
cholesky(B) # raises an exception, not positive definite---------------------------------------------------------------------------
LinAlgError Traceback (most recent call last)
Cell In[138], line 2
1 from numpy.linalg import cholesky
----> 2 cholesky(B) # raises an exception, not positive definite
File ~/mambaforge/envs/myst/lib/python3.13/site-packages/numpy/linalg/_linalg.py:848, in cholesky(a, upper)
845 signature = 'D->D' if isComplexType(t) else 'd->d'
846 with errstate(call=_raise_linalgerror_nonposdef, invalid='call',
847 over='ignore', divide='ignore', under='ignore'):
--> 848 r = gufunc(a, signature=signature)
849 return wrap(r.astype(result_t, copy=False))
File ~/mambaforge/envs/myst/lib/python3.13/site-packages/numpy/linalg/_linalg.py:107, in _raise_linalgerror_nonposdef(err, flag)
106 def _raise_linalgerror_nonposdef(err, flag):
--> 107 raise LinAlgError("Matrix is not positive definite")
LinAlgError: Matrix is not positive definiteIt’s not hard to manufacture an SPD matrix to try out the Cholesky factorization:
B = A.T @ A
R = cholesky(B)
print(R)[[11.22497216 0. 0. 0. ]
[ 6.05792148 4.27803545 0. 0. ]
[11.58132048 -0.27085567 3.71478843 0. ]
[ 5.79066024 -0.25230391 0.77209511 3.43634484]]
print(norm(R @ R.T - B) / norm(B))8.342995500069933e-17