Chapter 13 - Fundamentals of Numerical Computation

Functions¶

Create a tensor-product grid

tensorgrid.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def tensorgrid(x, y):
    """
    tensorgrid(x, y)

    Create a tensor grid for a rectangle from its 1d projections x and y.
    Returns a function to reshape a 2d array to a vector, a function to reshape 
    a vector into a 2d array, a function to evaluate a function on the grid, 
    two arrays to give the grid coordinates, and a boolean array to identify 
    the boundary points.
    """
    m, n = len(x) - 1, len(y) - 1
    vec = lambda U: U.T.flatten()
    unvec = lambda u: np.reshape(u, (n+1, m+1)).T
    mtx = lambda h: np.array([[h(xi ,yj) for yj in y] for xi in x])
    X = mtx(lambda x, y: x)
    Y = mtx(lambda x, y: y)

    # Identify boundary points.
    is_boundary = np.tile(True, (m+1, n+1))
    is_boundary[1:-1, 1:-1] = False
    
    return mtx, X, Y, vec, unvec, is_boundary

Solution of Poisson’s equation by finite differences

poissonfd.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def poissonfd(f, g, m, xspan, n, yspan):
    """
    poissonfd(f, g, m, xspan, n, yspan)

    Solve Poisson's equation on a rectangle by finite differences. Function f is the
    forcing function and function g gives the  Dirichlet boundary condition. The rectangle
    is the tensor product of intervals xspan and yspan,  and the discretization uses
    m+1 and n+1 points in the two coordinates.

    Return matrices of the solution values, and the coordinate functions, on the grid.
    """
    # Discretize the domain.
    x, Dx, Dxx = diffmat2(m, xspan)
    y, Dy, Dyy = diffmat2(n, yspan)
    mtx, X, Y, vec, unvec, is_boundary = tensorgrid(x, y)
    N = (m+1) * (n+1)    # total number of unknowns

    # Form the collocated PDE as a linear system.
    Dxx = sp.lil_matrix(Dxx)
    Dyy = sp.lil_matrix(Dyy)
    A = sp.kron(sp.eye(n+1, format="lil"), Dxx) + sp.kron(Dyy, sp.eye(m+1, format="lil"))
    b = vec(mtx(f))

    # Apply Dirichlet condition.
    idx = vec(is_boundary)
    scale = np.max(abs(A[n+1, :]))
    I = sp.eye(N, format="lil")
    A[idx, :] = scale * I[idx, :]         # Dirichet assignment
    X_bd, Y_bd = vec(X)[idx], vec(Y)[idx]
    b[idx] = scale * g(X_bd, Y_bd)    # assigned values

    # Solve the linear sytem and reshape the output.
    u = scipy.sparse.linalg.spsolve(A.tocsr(), b)
    U = unvec(u)
    return U, X, Y

Solution of elliptic PDE by Chebyshev collocation

elliptic.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def elliptic(f, g, m, xspan, n, yspan):
    """
    newtonpde(f, g, m, xspan, n, yspan)

    Newton's method with finite differences to solve the PDE f(u,x,y,disc)=0 on the
    rectangle xspan \times yspan, subject to g(x,y)=0 on the boundary. Use m+1
    points in x by n+1 points in y.

    Return matrices of the solution values, and the coordinate functions, on the grid.
    """
    from scipy.sparse.linalg import spsolve
    x, Dx, Dxx = diffcheb(m, xspan)
    y, Dy, Dyy = diffcheb(n, yspan)
    mtx, X, Y, vec, unvec, is_boundary = tensorgrid(x, y)

    # Evaluate the boundary condition at the boundary nodes.
    idx = vec(is_boundary)
    X_bd, Y_bd = vec(X)[idx], vec(Y)[idx]
    g_bd = g(X_bd, Y_bd)

    # Evaluate the PDE+BC residual.
    def residual(u):
        U = unvec(u)
        R = f(X, Y, U, Dx @ U, Dxx @ U, U @ Dy.T, U @ Dyy.T)    # PDE
        r = vec(R)
        r[idx] = u[idx] - g_bd                                  # BC
        return r
    
    # Solve the equation.
    u = levenberg(residual, vec(np.zeros(X.shape)))[-1]
    U = unvec(u)

    def evaluate(xi, eta):
        v = [chebinterp(y, u, eta) for u in U]
        return chebinterp(x, v, xi)
    
    return np.vectorize(evaluate)

Examples¶

13.1 Tensor-product discretizations¶

Example 13.1.2

Here is the grid from Example 13.1.1.

m = 4
x = linspace(0, 2, m+1)
n = 2
y = linspace(1, 3, n+1)

For a given $f(x,y)$ we can find $\operatorname{mtx}(f)$ by using a comprehension syntax.

f = lambda x, y: cos(pi * x * y - y)
F = array( [ [f(xi, yj) for yj in y] for xi in x ] )
print(F)

[[ 0.54030231 -0.41614684 -0.9899925 ]
 [ 0.84147098  0.41614684 -0.14112001]
 [-0.54030231 -0.41614684  0.9899925 ]
 [-0.84147098  0.41614684  0.14112001]
 [ 0.54030231 -0.41614684 -0.9899925 ]]

We can make a nice plot of the function by first choosing a much finer grid. However, the contour and surface plotting functions expect the transpose of mtx( $f$ ).

m, n = 80, 70
x = linspace(0, 2, m+1)
y = linspace(1, 3, n+1)
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)
F = mtx(f)

pcolormesh(X.T, Y.T, F.T, cmap="RdBu", vmin=-1, vmax=1, shading="gouraud")
axis("equal"),  colorbar()
xlabel("$x$"),  ylabel("$y$");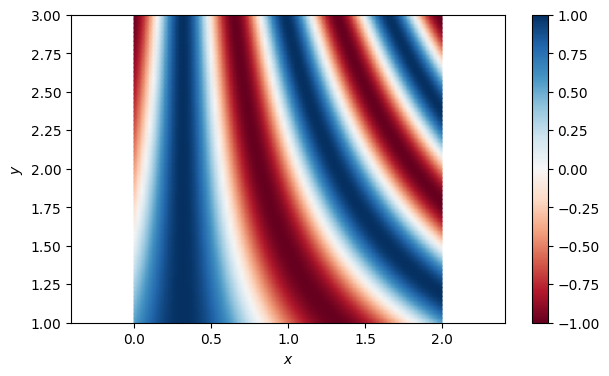

Example 13.1.3

For a function given in polar form, such as $f(r,\theta)=1-r^4$ , construction of a function over the unit disk is straightforward using a grid in $(r,\theta)$ space.

r = linspace(0, 1, 41)
theta = linspace(0, 2*pi, 121)
mtx, R, Theta, _, _, _ = FNC.tensorgrid(r, theta)

F = mtx(lambda r, theta: 1 - r**4)    

contourf(R.T, Theta.T, F.T, levels=20)
colorbar()
xlabel("$r$"),  ylabel("$\\theta$");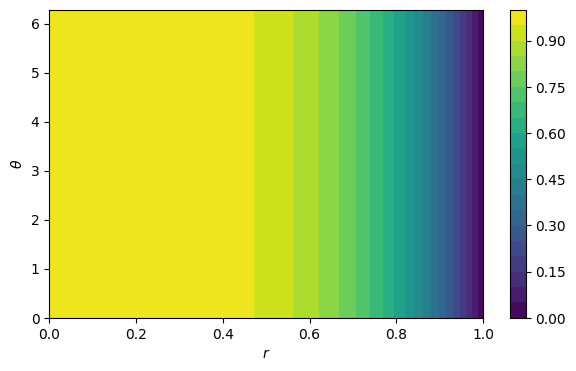

Of course, we are used to seeing such plots over the $(x,y)$ plane, not the $(r,\theta)$ plane. For this we create matrices for the coordinate functions $x$ and $y$ .

X, Y = R * cos(Theta), R * sin(Theta)
contourf(X.T, Y.T, F.T, levels=20)
colorbar(),  axis("equal")
xlabel("$x$"),  ylabel("$y$");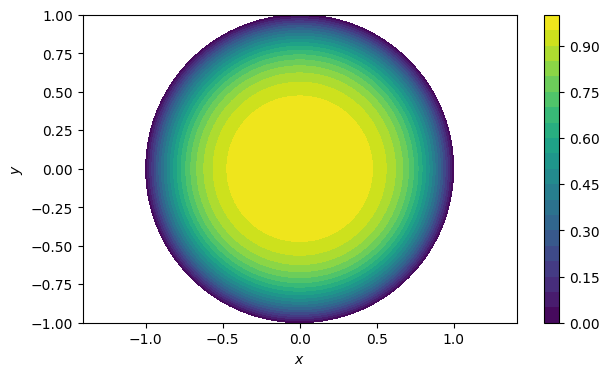

In such functions the values along the line $r=0$ must be identical, and the values on the line $\theta=0$ should be identical to those on $\theta=2\pi$ . Otherwise the interpretation of the domain as the unit disk is nonsensical. If the function is defined in terms of $x$ and $y$ , then those can be defined in terms of $r$ and θ using (13.1.6).

Example 13.1.4

We define a function and, for reference, its two exact partial derivatives.

u = lambda x, y: sin(pi * x * y - y)
du_dx = lambda x, y: pi * y * cos(pi * x * y - y)
du_dy = lambda x, y: (pi * x - 1) * cos(pi * x * y - y)

We will use an equispaced grid and second-order finite differences as implemented by diffmat2. First, we have a look at a plots of the exact partial derivatives.

m, n = 80, 60
x, Dx, Dxx = FNC.diffmat2(m, [0, 2])
y, Dy, Dyy = FNC.diffmat2(n, [1, 4])
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)

U = mtx(u)
dU_dX = mtx(du_dx)
dU_dY = mtx(du_dy)

subplot(1, 2, 1)
contourf(X.T, Y.T, dU_dX.T)
title("$u$"),  axis("equal")
subplot(1, 2, 2)
contourf(X.T, Y.T, dU_dY.T)
title("$\\partial u/\\partial y$"),  axis("equal");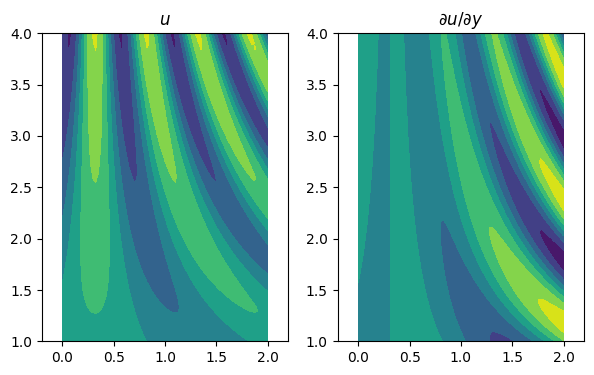

Now we compare the exact partial derivatives with their finite-difference approximations. Since these are signed errors, we use a colormap that is symmetric around zero.

subplot(1, 2, 1)
pcolormesh(X, Y, Dx @ U  - dU_dX, shading="gouraud", cmap="RdBu", vmin=-0.4, vmax=0.4)
colorbar()
title("error in $\\partial u/\\partial x$"),  axis("equal")
subplot(1, 2, 2)
pcolormesh(X, Y, U @ Dy.T - dU_dY, shading="gouraud", cmap="RdBu", vmin=-0.1, vmax=0.1)
colorbar()
title("error in $\\partial u/\\partial y$"),  axis("equal");

Not surprisingly, the errors are largest where the derivatives themselves are largest.

13.2 Two-dimensional diffusion and advection¶

Example 13.2.1

m, n = 4, 3
x = linspace(0, 2, m+1)
y = linspace(-3, 0, n+1)

f = lambda x, y: cos(0.75 * pi * x * y - 0.5 * pi * y)
mtx, X, Y, vec, unvec, _ = FNC.tensorgrid(x, y)
F = mtx(f)
print(f"function on a {m}x{n} grid:")
with printoptions(precision=4, suppress=True):
    print(F)

print("vec(F):")
with printoptions(precision=4, suppress=True):
    print(vec(F))

function on a 4x3 grid:
[[-0.     -1.      0.      1.    ]
 [ 0.3827  0.7071  0.9239  1.    ]
 [-0.7071  0.      0.7071  1.    ]
 [ 0.9239 -0.7071 -0.3827  1.    ]
 [-1.      1.     -1.      1.    ]]
vec(F):
[-0.      0.3827 -0.7071  0.9239 -1.     -1.      0.7071  0.     -0.7071
  1.      0.      0.9239  0.7071 -0.3827 -1.      1.      1.      1.
  1.      1.    ]

The unvec operation is the inverse of vec.

print("unvec(vec(F)):")
with printoptions(precision=4, suppress=True):
    print(unvec(vec(F)))

unvec(vec(F)):
[[-0.     -1.      0.      1.    ]
 [ 0.3827  0.7071  0.9239  1.    ]
 [-0.7071  0.      0.7071  1.    ]
 [ 0.9239 -0.7071 -0.3827  1.    ]
 [-1.      1.     -1.      1.    ]]

Example 13.2.2

m, n = 60, 40
x, Dx, Dxx = FNC.diffper(m, [-1, 1])
y, Dy, Dyy = FNC.diffper(n, [-1, 1])
mtx, X, Y, vec, unvec, _ = FNC.tensorgrid(x, y)

Note that the initial condition should also be periodic on the domain.

u_init = lambda x, y: sin(4 * pi * x) * exp(cos(pi * y))
U0 = mtx(u_init)
mx = max(abs(U0))
pcolormesh(X, Y, U0, vmin=-mx, vmax=mx, cmap="RdBu", shading="gouraud")
axis("equal"),  colorbar()
xlabel("$x$"),  ylabel("$y$")
title("Initial condition");

This function computes the time derivative for the unknowns. The actual calculations take place using the matrix shape.

alpha = 0.1
def du_dt(t, u):
    U = unvec(u)
    Uyy = Dxx @ U
    Uxx = U @ Dyy.T
    dU_dt = alpha * (Uxx + Uyy)  # PDE
    return vec(dU_dt)

Since this problem is parabolic, a stiff integrator is appropriate.

from scipy.integrate import solve_ivp
sol = solve_ivp(du_dt, (0, 0.2), vec(U0), method="BDF", dense_output=True)
U = lambda t: unvec(sol.sol(t))

pcolormesh(X.T, Y.T, U(0.02).T, 
    vmin=-mx, vmax=mx, cmap="RdBu", shading="gouraud")
axis("equal"),  colorbar()
xlabel("$x$"),  ylabel("$y$")
title("Heat equation, t=0.02");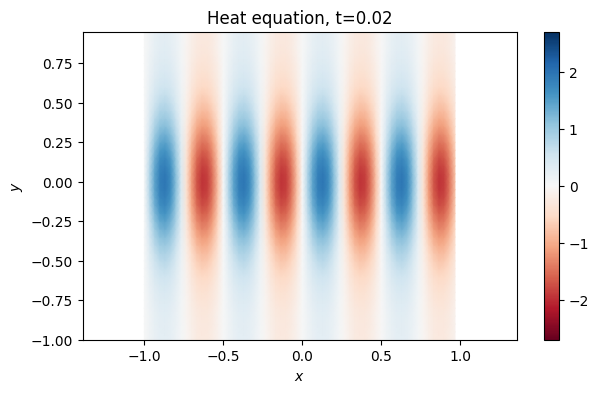

Here is an animation of the solution.

from matplotlib import animation
fig, ax = subplots()
obj = ax.pcolormesh(X, Y, U(0), vmin=-mx, vmax=mx, cmap="RdBu", shading="gouraud")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$"),  ax.set_ylabel("$y$")
ax.set_aspect("equal")
ax.set_title("Heat equation on a periodic domain")
def snapshot(t):
    global obj
    obj.remove()
    obj = ax.pcolormesh(X, Y, U(t), vmin=-mx, vmax=mx, cmap="RdBu", shading="gouraud")
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(fig, snapshot, frames=linspace(0, 0.2, 41))
anim.save("figures/heat-2d.mp4", fps=30)
close()

Example 13.2.3

The first step is to define a discretization of the domain.

m, n = 50, 36
x, Dx, Dxx = FNC.diffcheb(m, [-1, 1])
y, Dy, Dyy = FNC.diffcheb(n, [-1, 1])
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)
u_init = lambda x, y: (1 + y) * (1 - x)**4 * (1 + x)**2 * (1 - y**4)

There are really two grids now: the full grid and the subset grid of interior points. Since the IVP unknowns are on the interior grid, that is the one we need to change shapes on. We also need the functions extend and chop to add and remove boundary values.

_, _, _, vec, unvec, _ = FNC.tensorgrid(x[1:-1], y[1:-1])

def chop(U):
    return U[1:-1, 1:-1]

def extend(U):
    UU = zeros((m+1, n+1))
    UU[1:-1, 1:-1] = U
    return UU

pack = lambda U: vec(chop(U))          # restrict to interior, then vectorize
unpack = lambda u: extend(unvec(u))    # unvectorize, then extend to boundary

Now we can define and solve the IVP using a stiff solver.

ep = 0.05
def dw_dt(t, w):
    U = unpack(w)
    Uyy = Dxx @ U
    Uxx = U @ Dyy.T 
    dU_dt = 1 - Dx @ U + ep * (Uxx + Uyy)
    return pack(dU_dt)

U0 = mtx(u_init)
sol = solve_ivp(dw_dt, (0, 2), pack(U0), method="BDF", dense_output=True)

When we evaluate the solution at a particular value of $t$ , we get a vector of the interior grid values. The same unpack function above converts this to a complete matrix of grid values.

U = lambda t: unpack(sol.sol(t))    # function of time on the grid

pcolormesh(X.T, Y.T, U(0.5).T, cmap="Blues", shading="gouraud")
colorbar()
xlabel("$x$"),  ylabel("$y$")
axis("equal"),  title("Solution at t=0.5");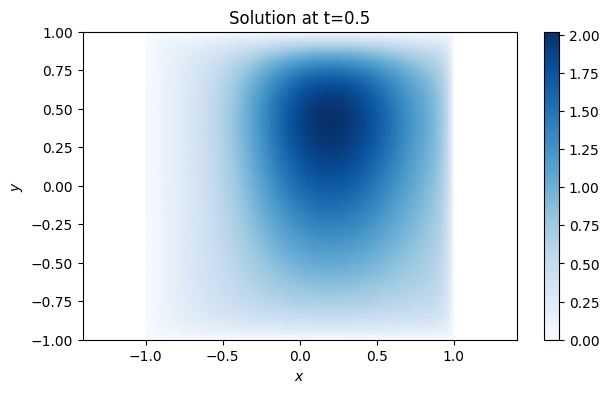

fig, ax = subplots()
obj = ax.pcolormesh(X.T, Y.T, U(0).T, vmin=0, vmax=2, cmap="Blues", shading="gouraud")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$"),  ax.set_ylabel("$y$")
ax.set_aspect("equal")
ax.set_title("Advection-diffusion in 2d")
def snapshot(t):
    global obj
    obj.remove()
    obj = ax.pcolormesh(X.T, Y.T, U(t).T, vmin=0, vmax=2, cmap="Blues", shading="gouraud")
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(fig, snapshot, frames=linspace(0, 2, 81))
anim.save("figures/advdiff-2d.mp4", fps=30)
close()

Example 13.2.4

We start with the discretization and initial condition.

m, n = 40, 42
x, Dx, Dxx = FNC.diffcheb(m, [-2, 2])
y, Dy, Dyy = FNC.diffcheb(n, [-2, 2])
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)

U0 = mtx(lambda x, y: (x + 0.2) * exp(-12 * (x**2 + y**2)))
V0 = zeros(U0.shape)

Note that because $u$ is known on the boundary, while $v$ is unknown over the full grid, there are two different sizes of vec/unvec operations. We also need to define functions to pack grid unknowns into a vector and to unpack them. When the unknowns for $u$ are packed, the boundary values are chopped off, and these are restored when unpacking.

_, _, _, vec_v, unvec_v, _ = FNC.tensorgrid(x, y)
_, _, _, vec_u, unvec_u, _ = FNC.tensorgrid(x[1:-1], y[1:-1])

def extend(U):
    UU = zeros((m+1, n+1))
    UU[1:-1, 1:-1] = U
    return UU

def chop(U):
    return U[1:-1, 1:-1]

def pack(U, V): 
    return hstack([vec_u(chop(U)), vec_v(V)])

N = (m-1) * (n-1)
def unpack(w):
    U = extend(unvec_u(w[:N]))
    V = unvec_v(w[N:])
    return U, V

We can now define and solve the IVP. Since this problem is hyperbolic, not parabolic, a nonstiff integrator is faster than a stiff one.

def dw_dt(t, w):
    U, V = unpack(w)
    dU_dt = V
    dV_dt = Dxx @ U + U @ Dyy.T
    return pack(dU_dt, dV_dt)

from scipy.integrate import solve_ivp
sol = solve_ivp(dw_dt, (0, 4), pack(U0, V0), method="RK45", dense_output=True)
U = lambda t: unpack(sol.sol(t))[0]

fig, ax = subplots()
obj = ax.pcolormesh(X, Y, U(0), vmin=-0.1, vmax=0.1, cmap="RdBu", shading="gouraud")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$"),  ax.set_ylabel("$y$")
ax.set_aspect("equal")
ax.set_title("Wave equation in 2d")

def snapshot(t):
    global obj
    obj.remove()
    obj = ax.pcolormesh(X, Y, U(t), vmin=-0.1, vmax=0.1, cmap="RdBu", shading="gouraud")
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(fig, snapshot, frames=linspace(0, 4, 91))
anim.save("figures/wave-2d.mp4", fps=30);
close()

13.3 Laplace and Poisson equations¶

Example 13.3.1

A = array([[1, 2], [-2, 0]])
B = array([[1, 10, 100], [-5, 5, 3]])
print("A:")
print(A)
print("B:")
print(B)

A:
[[ 1  2]
 [-2  0]]
B:
[[  1  10 100]
 [ -5   5   3]]

Applying the definition manually, we get

A_kron_B = vstack([ hstack([A[0, 0] * B, A[0, 1] * B]), hstack([A[1, 0] * B, A[1, 1] * B]) ])
print(A_kron_B)

[[   1   10  100    2   20  200]
 [  -5    5    3  -10   10    6]
 [  -2  -20 -200    0    0    0]
 [  10  -10   -6    0    0    0]]

But it makes more sense to use kron from NumPy, or the scipy.sparse version when sparsity is to be preserved.

kron(A, B)

array([[   1,   10,  100,    2,   20,  200],
       [  -5,    5,    3,  -10,   10,    6],
       [  -2,  -20, -200,    0,    0,    0],
       [  10,  -10,   -6,    0,    0,    0]])

Example 13.3.2

We make a crude discretization for illustrative purposes.

m, n = 5, 6
x, Dx, Dxx = FNC.diffmat2(m, [0, 3])
y, Dy, Dyy = FNC.diffmat2(n, [-1, 1])
mtx, X, Y, vec, unvec, is_boundary = FNC.tensorgrid(x, y)

Next, we define ϕ and evaluate it on the grid to get the forcing vector of the linear system.

f = lambda x, y: x**2 - y + 2
b = vec(mtx(f))

Here are the coefficients for the PDE collocation, before any modifications are made for the boundary conditions. The combination of Kronecker products and finite differences produces a characteristic sparsity pattern.

import scipy.sparse as sp
Dxx = sp.lil_matrix(Dxx)
Dyy = sp.lil_matrix(Dyy)
Ix = sp.eye(m+1)
Iy = sp.eye(n+1)
A = sp.kron(Iy, Dxx) + sp.kron(Dyy, Ix)

spy(A)
title("Matrix before imposing BC");

The number of equations is equal to $(m+1)(n+1)$ , which is the total number of points on the grid.

N = len(b)

We now use the Boolean array that indicates where the boundary points lie in the grid.

spy(is_boundary)
title("Boundary points");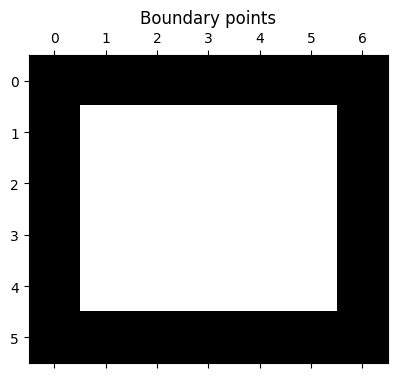

In order to impose Dirichlet boundary conditions, we replace the boundary rows of the system by rows of the identity.

I = sp.eye(N, format="lil")
idx = vec(is_boundary)
A = A.tolil()
A[idx, :] = I[idx, :];    # Dirichlet conditions

spy(A)
title("Matrix with Dirichlet BC imposed");

Finally, we must replace the rows in the vector $\mathbf{b}$ by the boundary values being assigned to the boundary points. Here, we let the boundary values be zero everywhere.

b[idx] = 0

Now we can solve for $\mathbf{u}$ and reinterpret it as the matrix-shaped $\mathbf{U}$ , the solution on our grid.

from scipy.sparse.linalg import spsolve
u = spsolve(A.tocsr(), b)
U = unvec(u)
with printoptions(precision=4, suppress=True):
    print(U)

[[ 0.      0.      0.      0.      0.      0.      0.    ]
 [ 0.     -0.5512 -0.8252 -0.8791 -0.7476 -0.451   0.    ]
 [ 0.     -0.9109 -1.3939 -1.5092 -1.3003 -0.7928  0.    ]
 [ 0.     -1.1788 -1.7957 -1.9513 -1.7021 -1.0607  0.    ]
 [ 0.     -1.1409 -1.6859 -1.8182 -1.6083 -1.0407  0.    ]
 [ 0.      0.      0.      0.      0.      0.      0.    ]]

Example 13.3.3

First we define the problem on $[0,1]\times[0,2]$ .

f = lambda x, y: -sin(3 * x * y - 4 * y) * (9 * y**2 + (3 * x - 4) ** 2)
g = lambda x, y: sin(3 * x * y - 4 * y)
xspan = [0, 1]
yspan = [0, 2]

Here is the finite-difference solution.

U, X, Y = FNC.poissonfd(f, g, 50, xspan, 80, yspan)

pcolormesh(X.T, Y.T, U.T, cmap="viridis")
xlabel("$x$"),  ylabel("$y$"),  axis("equal")
colorbar(), title("Solution of Poisson's equation");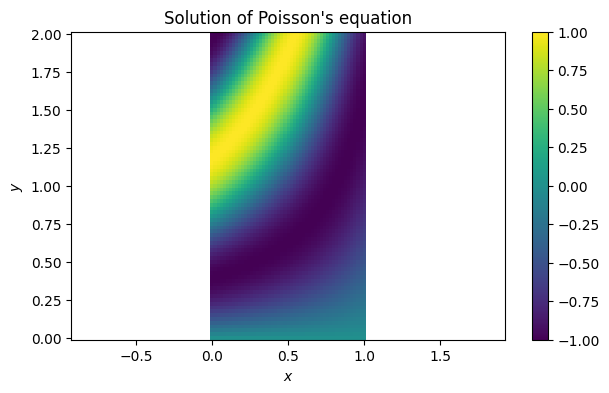

Since this is an artificial problem with a known solution, we can plot the error, which is a smooth function of $x$ and $y$ . It must be zero on the boundary; otherwise, we have implemented boundary conditions incorrectly.

error = g(X, Y) - U    # because we set up g as the exact solution
M = max(abs(error))

pcolormesh(X.T, Y.T, error.T, vmin=-M, vmax=M, cmap="RdBu")
xlabel("$x$"),  ylabel("$y$"),  axis("equal")
colorbar(),  title("Error");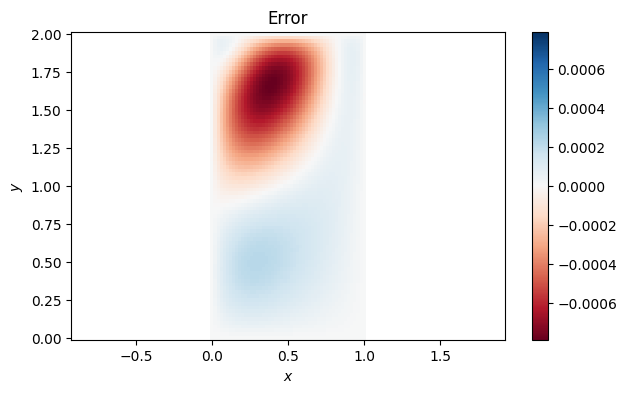

13.4 Nonlinear elliptic PDEs¶

Example 13.4.2

All we need to define are ϕ from (13.4.2) for the PDE, and a trivial zero function for the boundary condition.

lamb = 1.5
phi = lambda x, y, u, ux, uxx, uy, uyy: uxx + uyy - lamb / (u + 1)**2
g = lambda x, y: 0

Here is the solution for $m=15$ , $n=8$ .

u = FNC.elliptic(phi, g, 15, [0, 2.5], 8, [0, 1])

print(f"solution at (2, 0.6) is {u(2, 0.6):.7f}")

solution at (2, 0.6) is -0.2264594

x = linspace(0, 2.5, 90)
y = linspace(0, 1, 60)
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)
U = mtx(u)

pcolormesh(X.T, Y.T, U.T, cmap="viridis")
xlabel("$x$"),  ylabel("$y$"),  axis("equal")
colorbar()
title("Solution of the MEMS equation in 2d");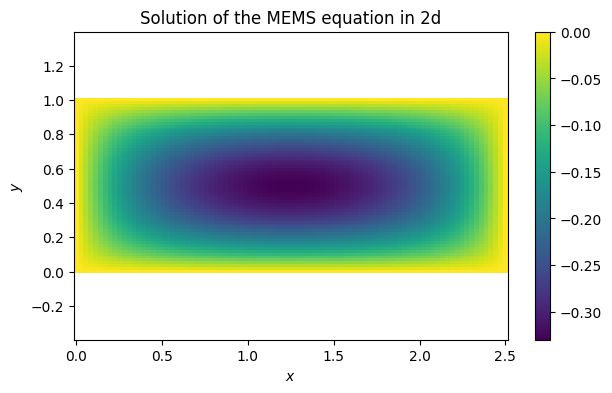

In the absence of an exact solution, how can we be confident that the solution is accurate? First, the Levenberg iteration converged without issuing a warning, so we should feel confident that the discrete equations were solved. We can check the boundary values easily. For example,

err = norm(u(x, 0) - g(x, 0), inf)
print(f"max error on bottom edge: {err:.2e}")

max error on bottom edge: 2.90e-23

Assuming that we encoded the PDE correctly, the remaining source error is truncation from the discretization. We can estimate that by refining the grid a bit and seeing how much the numerical solution changes.

x_test = linspace(0, 2.5, 6)
y_test = linspace(0, 1, 6)
mtx_test, X_test, Y_test, _, _, _ = FNC.tensorgrid(x_test, y_test)

with printoptions(precision=7, suppress=True):
    print(mtx_test(u))

[[ 0.         0.        -0.        -0.         0.         0.       ]
 [ 0.        -0.1479641 -0.2264594 -0.2264594 -0.1479641  0.       ]
 [ 0.        -0.1958612 -0.3059492 -0.3059492 -0.1958612  0.       ]
 [-0.        -0.1958612 -0.3059492 -0.3059492 -0.1958612  0.       ]
 [ 0.        -0.1479641 -0.2264594 -0.2264594 -0.1479641  0.       ]
 [ 0.         0.         0.         0.         0.         0.       ]]

u = FNC.elliptic(phi, g, 25, [0, 2.5], 14, [0, 1])
with printoptions(precision=7, suppress=True):
    print(mtx_test(u))

[[ 0.        -0.        -0.         0.         0.         0.       ]
 [-0.        -0.1479584 -0.226453  -0.226453  -0.1479584 -0.       ]
 [-0.        -0.195861  -0.3059293 -0.3059293 -0.195861  -0.       ]
 [-0.        -0.195861  -0.3059293 -0.3059293 -0.195861  -0.       ]
 [ 0.        -0.1479584 -0.226453  -0.226453  -0.1479584 -0.       ]
 [ 0.        -0.         0.        -0.        -0.         0.       ]]

The original solution seems to be accurate to about four digits.

Example 13.4.3

phi = lambda x, y, u, ux, uxx, uy, uyy: 1 - ux - 2*uy + 0.05 * (uxx + uyy)
g = lambda x, y: 0
u = FNC.elliptic(phi, g, 32, [-1, 1], 32, [-1, 1])

x = y = linspace(-1, 1, 70)
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)
U = mtx(u)

pcolormesh(X.T, Y.T, U.T, cmap="viridis")
xlabel("$x$"),  ylabel("$y$"),  axis("equal")
colorbar()
title("Steady advection–diffusion");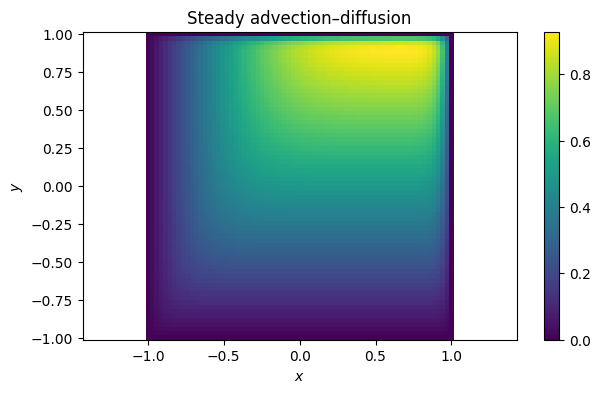

Example 13.4.4

The following defines the PDE and a nontrivial Dirichlet boundary condition for the square $[0,1]^2$ .

phi = lambda x, y, u, ux, uxx, uy, uyy: u * (1 - u**2) + 0.05 * (uxx + uyy)
g = lambda x, y: tanh(5 * (x + 2*y - 1))

We solve the PDE and then plot the result.

u = FNC.elliptic(phi, g, 36, [0, 1], 36, [0, 1])

x = y = linspace(0, 1, 70)
mtx, X, Y, _, _, _ = FNC.tensorgrid(x, y)
U = mtx(u)
pcolormesh(X.T, Y.T, U.T, cmap="viridis")
xlabel("$x$"),  ylabel("$y$"),  axis("equal")
colorbar(),  title("Steady Allen–Cahn equation");