Chapter 12 - Fundamentals of Numerical Computation

Examples¶

12.1 Traffic flow¶

In the following definition we allow the velocity $c$ to be specified as a parameter in the ODEProblem.

x, Dx, Dxx = FNC.diffper(300, [-4, 4])
f = lambda t, u: -c * (Dx @ u)

The following initial condition isn’t mathematically periodic, but the deviation is less than machine precision. We specify RK4 as the solver.

from scipy.integrate import solve_ivp
u_init = 1 + exp(-3 * x**2)
c = 2
sol = solve_ivp(f, [0, 3.0], u_init, method="Radau", dense_output=True)

for t in arange(0, 3, 2/3):
    plot(x, sol.sol(t), label=f"t = {t:.1f}")
legend()
xlabel("$x$"),  ylabel("$u(x,t)$")
title("Advection with periodic boundary");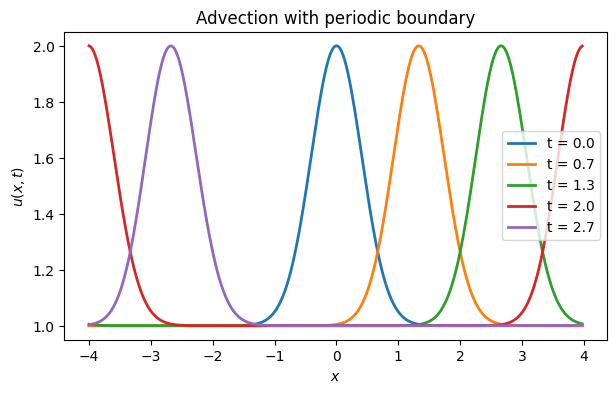

An animation shows the solution nicely. The bump moves with speed 2 to the right, reentering on the left as it exits to the right because of the periodic conditions.

from matplotlib import animation
fig, ax = subplots()
curve = ax.plot(x, u_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

ax.set_xlabel("$x$")
ax.set_ylabel("$u(x,t)$")
ax.set_ylim(0.9, 2.1)
ax.set_title("Advection equation with periodic boundary")

def snapshot(t):
    curve.set_ydata(sol.sol(t))
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 3, 201)
    )
anim.save("figures/advection-periodic.mp4", fps=30)
close()

Example 12.1.2

The following are parameters and a function relevant to defining the problem.

rho_c = 1080
rho_m = 380
q_m = 10000
Q0prime = (
    lambda rho: q_m
    * 4
    * rho_c**2
    * (rho_c - rho_m)
    * rho_m
    * (rho_m - rho)
    / (rho * (rho_c - 2 * rho_m) + rho_c * rho_m) ** 3
)

Here we create a discretization on $m=800$ points.

x, Dx, Dxx = FNC.diffper(800, [0, 4])

Next we define the ODE resulting from the method of lines.

ode = lambda t, rho: -Q0prime(rho) * (Dx @ rho) + ep * (Dxx @ rho)

Our first initial condition has moderate density with a small bump. Because of the diffusion present, we use a stiff solver for the IVP.

rho_init = 400 + 10 * exp(-20 * (x - 3) ** 2)
ep = 0.02
sol = solve_ivp(ode, [0, 1.0], rho_init, method="Radau", dense_output=True)

for t in linspace(0, 1, 6):
    plot(x, sol.sol(t), label=f"t = {t:.1f}")

xlabel("$x$"),  ylabel("car density")
legend(),  title("Traffic flow");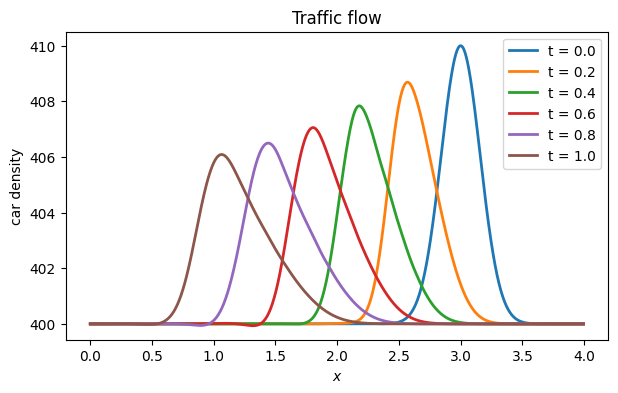

The bump slowly moves backward on the roadway, spreading out and gradually fading away due to the presence of diffusion.

fig, ax = subplots()
curve = ax.plot(x, rho_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("density")
ax.set_ylim(400, 410)
ax.set_title("Traffic flow")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 1, 101)
    )
anim.save("figures/traffic-small.mp4", fps=30)
close()

Now we use an initial condition with a larger bump. Note that the scale on the $y$ -axis is much different for this solution.

rho_init = 400 + 80 * exp(-16 * (x - 3) ** 2)
sol = solve_ivp(ode, [0, 0.5], rho_init, method="Radau", dense_output=True)

for t in linspace(0, 0.5, 6):
    plot(x, sol.sol(t), label=f"t = {t:.1f}")

xlabel("$x$"),  ylabel("car density")
legend(),  title("Traffic jam");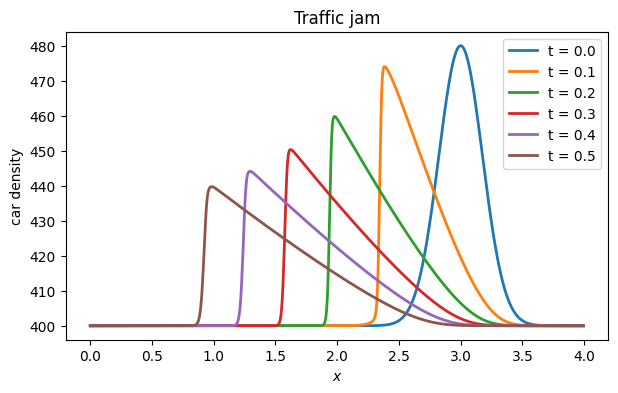

fig, ax = subplots()
curve = ax.plot(x, rho_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("density")
ax.set_ylim(400, 480)
ax.set_title("Traffic jam")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 0.5, 101)
    )
anim.save("figures/traffic-jam.mp4", fps=30)
close()

In this case the density bump travels backward along the road. It also steepens on the side facing the incoming traffic and decreases much more slowly on the other side. A motorist would experience this as an abrupt increase in density, followed by a much more gradual decrease in density and resulting gradual increase in speed. (You also see some transient, high-frequency oscillations. These are caused by instabilities, as we discuss in simpler situations later in this chapter.)

12.2 Upwinding and stability¶

Example 12.2.3

For time stepping, we use the adaptive explicit method RK45.

x, Dx, Dxx = FNC.diffper(400, [0, 1])
u_init = exp(-80 * (x - 0.5) ** 2)
c = 2
ode = lambda t, u: -c * (Dx @ u)
sol = solve_ivp(ode, (0, 2), u_init, method="RK45", dense_output=True)
u = sol.sol

t = linspace(0, 2, 81)
U = vstack([u(tj) for tj in t])
contour(x, t, U, levels=arange(0.15, 1.0, 0.2))
xlabel("$x$"),  ylabel("$t$")
title("Linear advection");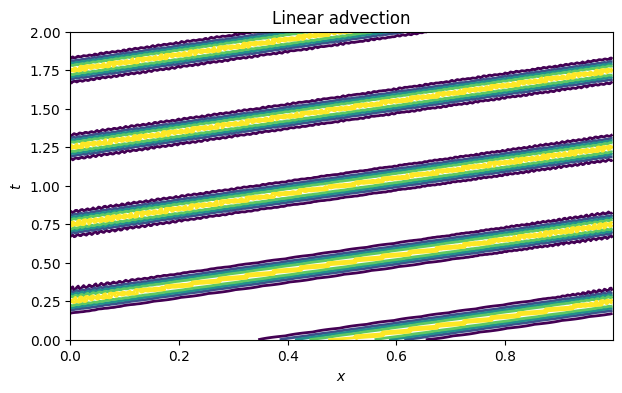

In the space-time plot above, you can see the initial hump traveling rightward at constant speed. It fully traverses the domain once for each integer multiple of $t=1/2$ .

If we cut $h$ by a factor of 2 (i.e., double $m$ ), then the CFL condition suggests that the time step should be cut by a factor of 2 also.

print(f"{len(sol.t) - 1} time steps taken for m = 400")

x, Dx, Dxx = FNC.diffper(800, [0, 1])
u_init = exp(-80 * (x - 0.5) ** 2)
sol = solve_ivp(ode, (0, 2), u_init, method="RK45", dense_output=True)
print(f"{len(sol.t) - 1} time steps taken for m = 800")

1416 time steps taken for m = 400

2906 time steps taken for m = 800

Example 12.2.6

If we solve advection over $[0,1]$ with velocity $c=-1$ , the right boundary is in the upwind/inflow direction. Thus a well-posed boundary condition is $u(1,t)=0$ .

We’ll pattern a solution after Function 11.5.2. Since $u(x_m,t)=0$ , we define the ODE interior problem (11.5.4) for $\mathbf{v}$ without $u_m$ . For each evaluation of $\mathbf{v}'$ , we must extend the data back to $x_m$ first.

m = 80
x, Dx, Dxx = FNC.diffmat2(m, [0, 1])

chop = lambda u : u[:-1]
extend = lambda v: hstack([v, 0])

ode = lambda t, v: -c * chop( Dx @ extend(v) )
c = -1

Now we solve for an initial condition that has a single hump.

u_init = exp(-80 * (x - 0.5) ** 2)
sol = solve_ivp(ode, (0, 1), chop(u_init), method="RK45", dense_output=True)
u = lambda t: extend(sol.sol(t))

t = linspace(0, 1, 80)
U = [u(tj) for tj in t]
contour(x, t, U, levels=arange(0.15, 1.0, 0.2))
xlabel("$x$"),  ylabel("$t$")
title("Advection with inflow BC");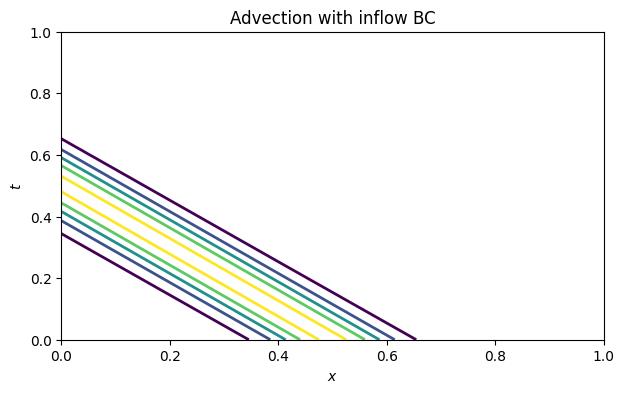

We find that the hump gracefully exits out the downwind end.

from matplotlib import animation
fig, ax = subplots()
curve = ax.plot(x, u_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("$u(x,t)$")
ax.set_ylim(-0.1, 1.1)
ax.set_title("Advection with inflow BC")

def snapshot(t):
    curve.set_ydata(u(t))
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 1, 101)
    )
anim.save("figures/advection-inflow.mp4", fps=30)
close()

If, instead of $u(1,t)=0$ , we were to try to impose the downwind condition $u(0,t)=0$ , we only need to change the index of the interior nodes and where to append the zero value.

chop = lambda u : u[1:]
extend = lambda v: hstack([0, v])

sol = solve_ivp(ode, (0, 1), chop(u_init), method="RK45", dense_output=True)
u = lambda t: extend(sol.sol(t))

U = [u(tj) for tj in t]
clf
contour(x, t, U, levels=arange(0.15, 1.0, 0.2))
xlabel("$x$"),  ylabel("$t$")
title("Outflow boundary condition");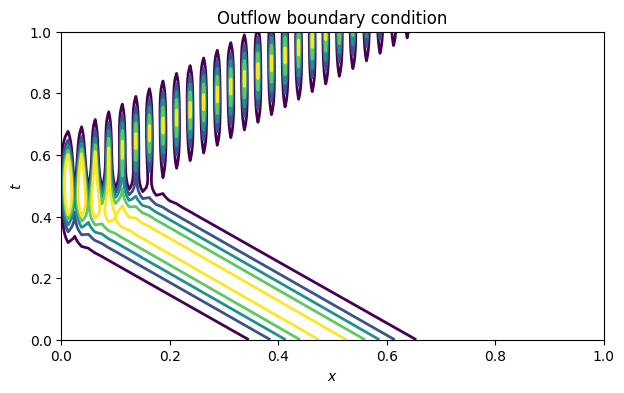

This time, the solution blows up as soon as the hump runs into the boundary because there are conflicting demands there.

fig, ax = subplots()
curve = ax.plot(x, u_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("$u(x,t)$")
ax.set_ylim(-0.1, 1.1)
ax.set_title("Advection with outflow BC")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 0.5, 51)
    )
anim.save("figures/advection-outflow.mp4", fps=30)
close()

12.3 Absolute stability¶

Example 12.3.1

For $c=1$ we get purely imaginary eigenvalues.

from scipy.linalg import eigvals
x, Dx, Dxx = FNC.diffper(40, [0, 1])
lamb = eigvals(Dx)

plot(real(lamb), imag(lamb), "o")
axis([-40, 40, -40, 40])
axis("equal")
title("Eigenvalues for pure advection");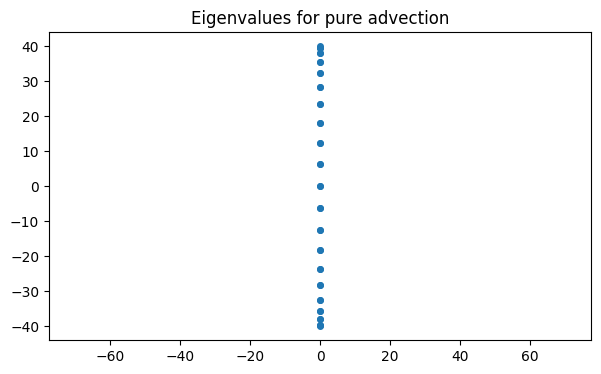

Let’s choose a time step of $\tau=0.1$ and compare to the stability regions of the Euler and backward Euler time steppers (shown as shaded regions):

zc = exp(2j * pi * arange(361) / 360)
# points on |z|=1

z = zc - 1    # shift circle left by 1
fill(real(z), imag(z), color=(0.8, 0.8, 1))
plot(real(0.1 * lamb), imag(0.1 * lamb), "o")
axis([-5, 5, -5, 5]),  axis("equal")
title("Euler");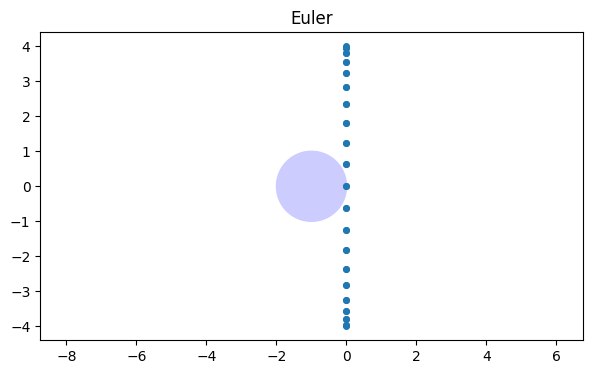

In the Euler case it’s clear that no real value of $\tau>0$ is going to make ζ values fit within the stability region. Any method whose stability region includes none of the imaginary axis is an unsuitable choice for advection.

z = zc + 1    # shift circle right by 1
fill([-6, 6, 6, -6], [-6, -6, 6, 6], color=(0.8, 0.8, 1))
fill(real(z), imag(z), color="w")
plot(real(0.1 * lamb), imag(0.1 * lamb), "o")
axis([-5, 5, -5, 5])
axis("equal")
title("Backward Euler");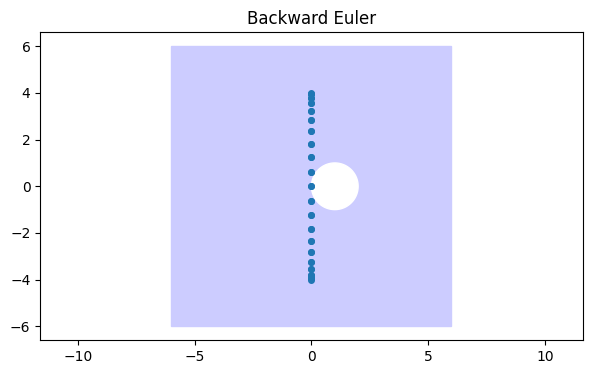

The A-stable backward Euler time stepping tells the exact opposite story: it will be absolutely stable for any choice of the time step τ.

Example 12.3.2

The eigenvalues of advection-diffusion are near-imaginary for $\epsilon\approx 0$ and get closer to the negative real axis as ε increases.

x, Dx, Dxx = FNC.diffper(40, [0, 1])
tau = 0.1
for ep in [0.001, 0.01, 0.05]:
    lamb = eigvals(-Dx + ep * Dxx)
    plot(real(tau * lamb), imag(tau * lamb), "o", label=f"epsilon={ep:.1g}")
axis("equal")
legend()
title("Eigenvalues for advection-diffusion");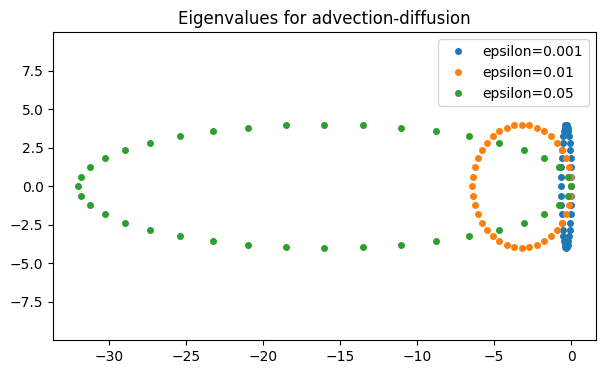

Example 12.3.3

Deleting the last row and column places all the eigenvalues of the discretization into the left half of the complex plane.

from scipy.linalg import eigvals
x, Dx, Dxx = FNC.diffcheb(40, [0, 1])
A = -Dx[1:, 1:]  # leave out first row and column

lamb = eigvals(A)
plot(real(lamb), imag(lamb), "o")
xlim(-300, 100),  axis("equal"),  grid(True)
title("Eigenvalues of advection with zero inflow");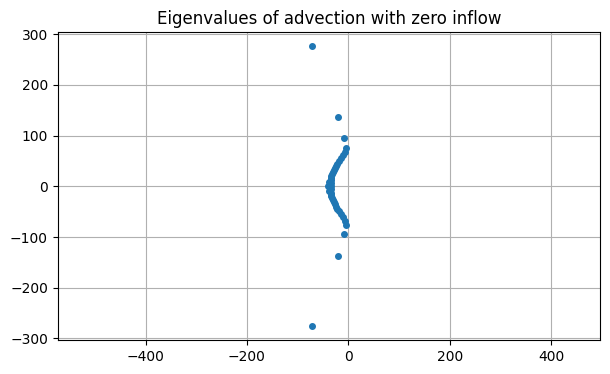

Note that the rightmost eigenvalues have real part at most

print(f"rightmost extent of eigenvalues: {max(real(lamb)):.3g}")

rightmost extent of eigenvalues: -4.93

Consequently all solutions decay exponentially to zero as $t\to\infty$ . This matches our observation of the solution: eventually, everything flows out of the domain.

12.4 The wave equation¶

Example 12.4.1

m = 200
x, Dx, Dxx = FNC.diffmat2(m, [-1, 1])

The boundary values of $u$ are given to be zero, so they are not unknowns in the ODEs. Instead they are added or removed as necessary.

chop = lambda u: u[1:-1]
extend = lambda v: hstack([0, v, 0])

The following function computes the time derivative of the system at interior points.

def dw_dt(t, w):
    u = extend(w[:m-1])
    z = w[m-1:]
    du_dt = Dx @ z
    dz_dt = c**2 * (Dx @ u)
    return hstack([chop(du_dt), dz_dt])

Our initial condition is a single hump for $u$ .

u_init = exp(-100 * x**2)
z_init = -u_init
w_init = hstack([chop(u_init), z_init])

Because the wave equation is hyperbolic, we can use a nonstiff explicit solver.

c = 2
sol = solve_ivp(dw_dt, (0, 2), w_init, dense_output=True)
u = lambda t: extend(sol.sol(t)[:m-1])   # extract the u component

We plot the results for the original $u$ variable only. Its interior values are at indices 1:m-1 of the composite $\mathbf{w}$ variable.

t = linspace(0, 2, 80)
U = [u(tj) for tj in t]
contour(x, t, U, levels=24, cmap="RdBu", vmin=-1, vmax=1)
xlabel("$x$"),  ylabel("$t$")
title("Wave equation with boundaries");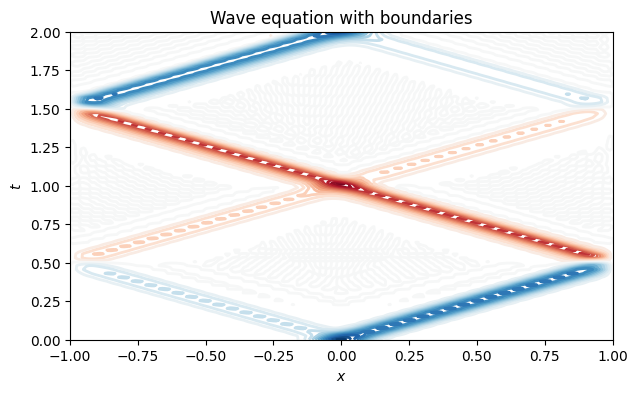

from matplotlib import animation
fig, ax = subplots()
curve = ax.plot(x, u_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("$u(x,t)$")
ax.set_ylim(-1.05, 1.05)
ax.set_title("Wave equation with boundaries")

def snapshot(t):
    curve.set_ydata(u(t))
    time_text.set_text(f"t = {t:.2f}")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 2, 161)
    )
anim.save("figures/wave-boundaries.mp4", fps=30)
close()

The original hump breaks into two pieces of different amplitudes, each traveling with speed $c=2$ . They pass through one another without interference. When a hump encounters a boundary, it is perfectly reflected, but with inverted shape. At time $t=2$ , the solution looks just like the initial condition.

Example 12.4.2

The variable wave speed is set to be re-used

m = 120
x, Dx, Dxx = FNC.diffcheb(m, [-1, 1])
c = 1 + (sign(x) + 1) / 2
u_init = exp(-100 * x**2)
z_init = -u_init
w_init = hstack([chop(u_init), z_init])

sol = solve_ivp(dw_dt, (0, 5), w_init, dense_output=True, method="Radau")
u = lambda t: extend(sol.sol(t)[:m-1])

t = linspace(0, 5, 150)
U = [u(tj) for tj in t]
contour(x, t, U, levels=24, cmap="RdBu", vmin=-1, vmax=1)
xlabel("$x$"),  ylabel("$t$")
title("Wave equation with variable speed");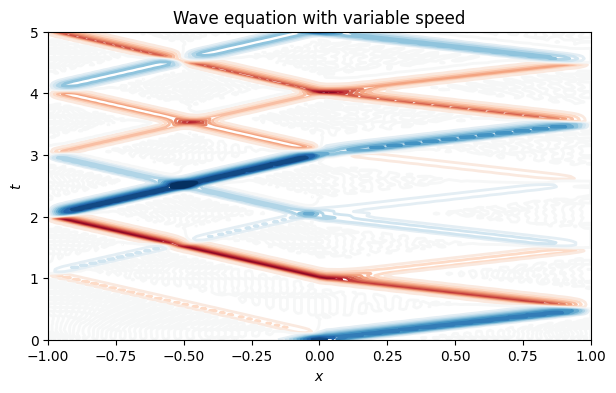

fig, ax = subplots()
curve = ax.plot(x, u_init)[0]
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel("$x$")
ax.set_ylabel("$u(x,t)$")
ax.set_ylim(-1.05, 1.05)
ax.set_title("Wave equation with variable speed")

anim = animation.FuncAnimation(
    fig, snapshot, frames=linspace(0, 5, 251)
    )
anim.save("figures/wave-speed.mp4", fps=30)
close()

Each pass through the interface at $x=0$ generates a reflected and transmitted wave. By conservation of energy, these are both smaller in amplitude than the incoming bump.