Chapter 11 - Fundamentals of Numerical Computation

Functions¶

Differentiation matrices for periodic end conditions

diffper.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def diffper(n, xspan):
    """
    diffper(n, xspan)

    Construct 2nd-order differentiation matrices for functions with periodic end
    conditions, using `n` unique nodes in the interval `xspan`. Return a vector of
    nodes and the  matrices for the first and second derivatives.
    """
    a, b = xspan
    h = (b - a) / n
    x = a + h * np.arange(n)  # nodes, omitting the repeated data

    # Construct Dx by diagonals, then correct the corners.
    dp = 0.5 / h * np.ones(n - 1)  # superdiagonal
    dm = -0.5 / h * np.ones(n - 1)  # subdiagonal
    Dx = np.diag(dm, -1) + np.diag(dp, 1)
    Dx[0, -1] = -1 / (2 * h)
    Dx[-1, 0] = 1 / (2 * h)

    # Construct Dxx by diagonals, then correct the corners.
    d0 = -2 / h**2 * np.ones(n)  # main diagonal
    dp = np.ones(n - 1) / h**2  # superdiagonal and subdiagonal
    Dxx = np.diag(d0) + np.diag(dp, -1) + np.diag(dp, 1)
    Dxx[0, -1] = 1 / (h**2)
    Dxx[-1, 0] = 1 / (h**2)

    return x, Dx, Dxx

Solution of parabolic PDEs by the method of lines

parabolic.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def parabolic(phi, xspan, m, ga, gb, tspan, init):
    """
        parabolic(phi, xspan, m, ga, gb, tspan, init)

    Solve a parabolic PDE by the method of lines. The PDE is 
    ∂u/∂t = phi(t,x,u,∂u/∂x,∂^2u/∂x^2), xspan gives the space 
    domain, m gives the degree of a Chebyshev spectral discretization, ga and gb are functions of (u,∂u/∂x) at the domain ends that should be made zero, tspan is the time domain, and init is a function of x that gives the initial condition. Returns a vector x and a function of t that gives the semidiscrete solution at x. 
    """   
    x, Dx, Dxx = diffcheb(m, xspan)
    int = range(1, m)    # indexes of interior nodes

    def extend(v):
        def objective(ubc):
            u0, um = ubc
            ux = Dx @ np.hstack([u0, v, um])
            return np.array([ga(u0, ux[1]), gb(um, ux[-1])])
        ubc = levenberg(objective, np.array([0, 0]))[-1]
        return np.hstack([ubc[0], v, ubc[-1]])

    def ode(t, v):
        u = extend(v)
        ux, uxx = Dx @ u, Dxx @ u
        return phi(t, x[int], u[int], ux[int], uxx[int])

    u0 = init(x[int])
    sol = solve_ivp(ode, tspan, u0, method="BDF", dense_output=True)

    return x, lambda t: extend(sol.sol(t))

Examples¶

11.1 Black–Scholes equation¶

Example 11.1.2

We consider the Black–Scholes problem for the following parameter values:

Smax, T = 8, 6
K = 3
sigma = 0.06
r = 0.08

We discretize space and time.

m = 200
h = Smax / m
x = h * arange(m+1)
n = 1000
tau = T / n
t = tau * arange(n+1)
lamb, mu = tau / h**2, tau / h

We set the initial condition and then march forward in time.

V = zeros([m + 1, n + 1])
V[:, 0] = maximum(0, x - K)
for j in range(n):
    # Fictitious value from Neumann condition.
    Vfict = 2 * h + V[m-1, j]
    Vj = hstack([V[:, j], Vfict])
    # First row is zero by the Dirichlet condition.
    for i in range(1, m+1):
        diff1 = Vj[i+1] - Vj[i-1]
        diff2 = Vj[i+1] - 2 * Vj[i] + Vj[i-1]
        V[i, j+1] = (
            Vj[i]
            + (lamb * sigma**2 * x[i] ** 2 / 2) * diff2
            + (r * x[i] * mu) / 2 * diff1
            - r * tau * Vj[i]
        )

Here is a plot of the solution after every 250 time steps.

select_times = 250 * arange(5)
show_times = t[select_times]

for j, col in enumerate(select_times):
    plot(x, V[:, col], label=f"t={show_times[j]:.1f}")

legend()
xlabel("stock price"),  ylabel("option value")
title("Black-Scholes solution");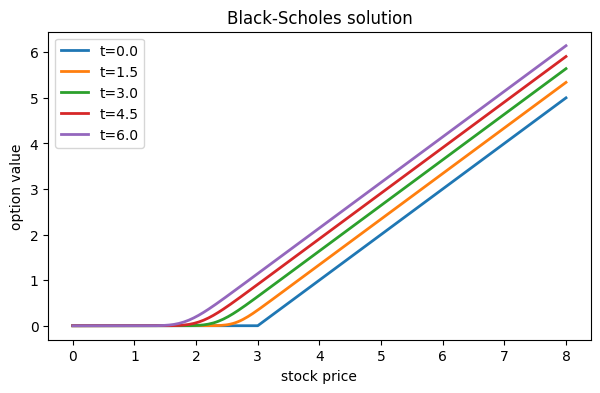

Alternatively, here is an animation of the solution.

from matplotlib import animation
fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, 8), ylim=(0, 6))
ax.grid()
ax.set_title("Black-Scholes solution")

line, = ax.plot([], [], '-', lw=2)
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

def animate(j):
    line.set_data(x, V[:, j])
    time_text.set_text(f"t = {t[j]:.2f}")
    return line, time_text

anim = animation.FuncAnimation(
    fig, animate, frames=range(0, n+1, 10), blit=True);
anim.save("figures/black-scholes-6.mp4", fps=30)
close()

The results are easy to interpret, recalling that the time variable really means time until strike. Say you are close to the option’s strike time. If the current stock price is, say, $S=2$ , then it’s not likely that the stock will end up over the strike price $K=3$ , and therefore the option has little value. On the other hand, if presently $S=3$ , then there are good odds that the option will be exercised at the strike time, and you will need to pay a substantial portion of the stock price in order to take advantage. As the time to strike increases, there is an expectation that the stock price is more likely to rise somewhat, making the value of the option larger at each fixed $S$ .

Example 11.1.3

Let’s try to do everything the same as in Demo 11.1.2, but extending the simulation time to $T=8$ .

T = 8
n = 1000;  tau = T / n
t = tau * arange(n + 1)
lamb, mu = tau / h**2, tau / h

V = zeros([m+1, n+1])
V[:, 0] = maximum(0, x - K)
for j in range(n):
    # Fictitious value from Neumann condition.
    Vfict = 2 * h + V[m - 1, j]
    Vj = hstack([V[:, j], Vfict])
    # First row is zero by the Dirichlet condition.
    for i in range(1, m + 1):
        diff1 = Vj[i + 1] - Vj[i - 1]
        diff2 = Vj[i + 1] - 2 * Vj[i] + Vj[i - 1]
        V[i, j + 1] = (
            Vj[i]
            + (lamb * sigma**2 * x[i] ** 2 / 2) * diff2
            + (r * x[i] * mu) / 2 * diff1
            - r * tau * Vj[i]
        )

select_times = 250 * arange(5)
show_times = t[select_times]

for j, col in enumerate(select_times):
    plot(x, V[:, col], label=f"t={show_times[j]:.1f}")

legend()
xlabel("stock price")
ylim([0, 6]);  ylabel("option value")
title("Black-Scholes solution");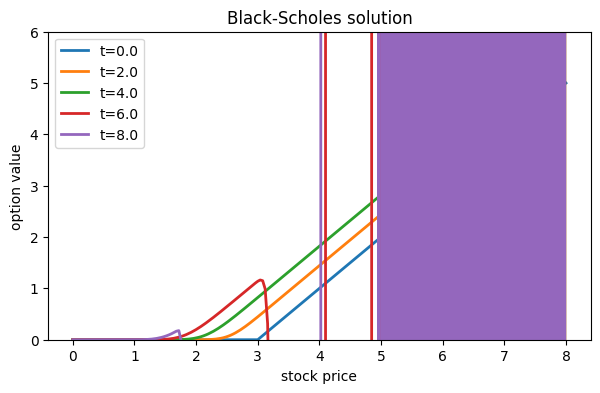

from matplotlib import animation
fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, 8), ylim=(0, 6))
ax.grid()
ax.set_title("Black-Scholes solution...?")

line, = ax.plot([], [], '-', lw=2)
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

def animate(j):
    line.set_data(x, V[:, j])
    time_text.set_text(f"t = {t[j]:.2f}")
    return line, time_text

anim = animation.FuncAnimation(
    fig, animate, frames=range(0, n+1), blit=True);
anim.save("figures/black-scholes-8.mp4", fps=24)
close()

This so-called solution is nonsense!

11.2 The method of lines¶

Example 11.2.2

Let’s implement the method of Example 11.2.1 with second-order space semidiscretization.

m = 100
x, Dx, Dxx = FNC.diffper(m, [0, 1])

tfinal = 0.15  
n = 2400                 # number of time steps  
tau = tfinal / n         # time step
t = tau * arange(n+1)    # time values

Next we set an initial condition. It isn’t mathematically periodic, but the end values and derivatives are so small that for numerical purposes it may as well be.

U = zeros([m, n+1])
U[:, 0] = exp(-60 * (x - 0.5) ** 2)
plot(x, U[:, 0])
xlabel("x");  ylabel("u(x,0)")
title("Initial condition");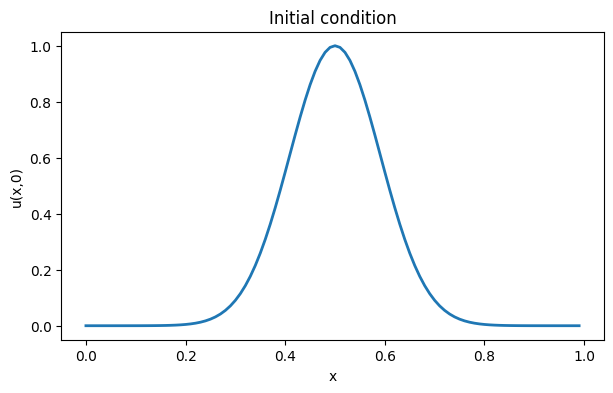

The Euler time stepping simply multiplies the solution vector by the constant matrix in (11.2.6) at each time step. Since that matrix is sparse, we will declare it as such, even though the run-time savings may not be detectable for this small value of $m$ .

import scipy.sparse as sp
I = sp.eye(m)
A = I + tau * sp.csr_array(Dxx)
for j in range(n):
    U[:, j+1] = A @ U[:, j]

plot(x, U[:, :31:10])
ylim([-0.25, 1])
xlabel("$x$");  ylabel("$u(x,t)$")
legend([f"$t={tj:.2e}$" for tj in t[:60:20]])
title("Heat equation by forward Euler");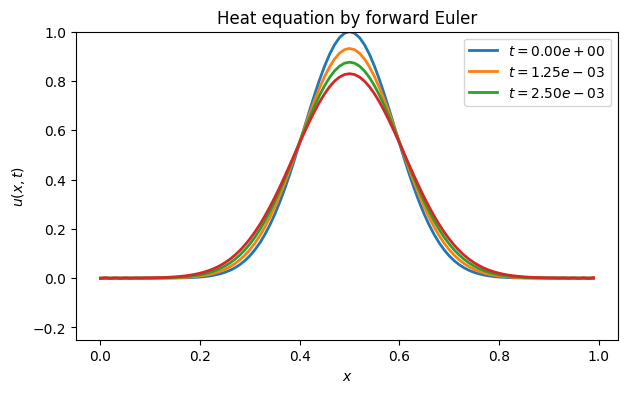

You see above that things seem to start well, with the initial peak widening and shrinking. But then there is a nonphysical growth in the solution.

from matplotlib import animation
fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, 1), ylim=(-1, 2))
ax.grid()

line, = ax.plot([], [], '-', lw=2)
ax.set_title("Heat equation by forward Euler")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

def animate(j):
    line.set_data(x, U[:, j])
    time_text.set_text(f"t = {t[j]:.2e}")
    return line, time_text

anim = animation.FuncAnimation(
    fig, animate, frames=range(0, 100), blit=True)
anim.save("figures/diffusionFE.mp4", fps=24)
close()

The growth in norm is exponential in time.

M = abs(U).max(axis=0)  # max in each column
semilogy(t[:500], M[:500])
xlabel("$t$");  ylabel("$\\max_x |u(x,t)|$")
title("Nonphysical growth");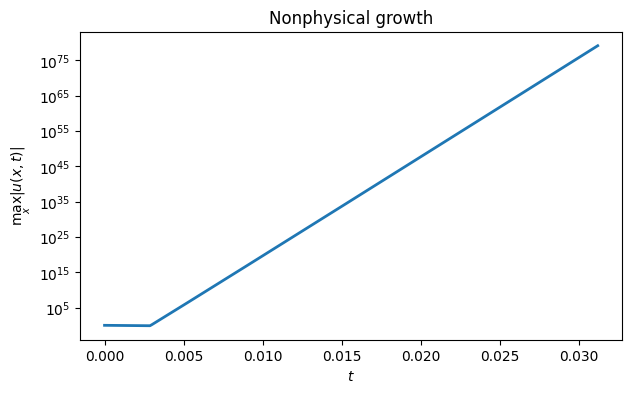

Example 11.2.4

Now we apply backward Euler to the heat equation. Mathematically this means multiplying by the inverse of a matrix, but we interpret that numerically as a linear system solution. We will reuse the setup from Demo 11.2.2.

from scipy.sparse.linalg import spsolve
B = sp.csr_matrix(I - tau * Dxx)
for j in range(n):
    U[:, j + 1] = spsolve(B, U[:, j])

plot(x, U[:, ::500])
xlabel("$x$")
ylabel("$u(x,t)$")
legend([f"$t={tj:.2g}$" for tj in t[::500]])
title("Heat equation by backward Euler");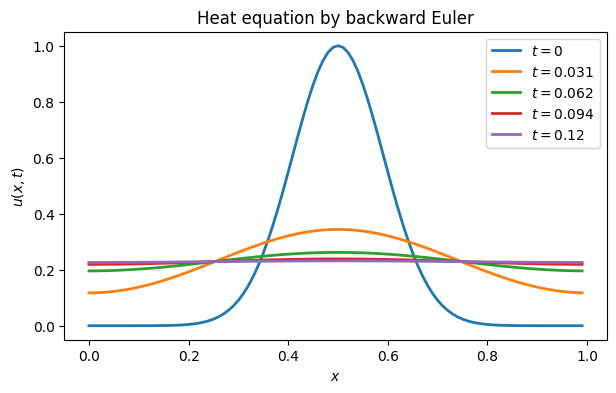

fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, 1), ylim=(-0.25, 1))
ax.grid()

line, = ax.plot([], [], '-', lw=2)
ax.set_title("Backward Euler")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

anim = animation.FuncAnimation(
    fig, animate, frames=range(0, n+1, 20), blit=True)
anim.save("figures/diffusionBE.mp4", fps=30)
close()

This solution looks physically plausible, as the large concentration in the center diffuses outward until the solution is essentially constant. Observe that the solution remains periodic in space for all time.

Example 11.2.5

We set up the semidiscretization and initial condition in $x$ just as before.

m = 100
x, Dx, Dxx = FNC.diffper(m, [0, 1])
u0 = exp(-60 * (x - 0.5) ** 2)

Now, however, we apply a standard solver using solve_ivp to the initial-value problem $\mathbf{u}'=\mathbf{D}_{xx}\mathbf{u}$ .

from scipy.integrate import solve_ivp
tfinal = 0.05
f = lambda t, u: Dxx @ u
sol = solve_ivp(f, [0, tfinal], u0, method="RK45", dense_output=True)

t = linspace(0, 0.05, 5)
plot(x, sol.sol(t))
xlabel("$x$"),  ylabel("$u(x,t)$")
legend([f"$t={tj:.4g}$" for tj in t])
title("Heat equation by RK45");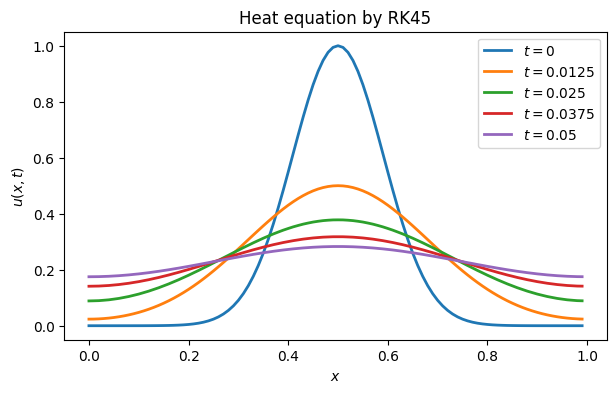

The solution appears to be correct. But the number of time steps that were selected automatically is surprisingly large, considering how smoothly the solution changes.

print(f"RK45 took {len(sol.t) - 1} steps")

RK45 took 602 steps

Now we apply a different solver called BDF.

sol = solve_ivp(f, [0, tfinal], u0, method="BDF")
print(f"BDF took {len(sol.t) - 1} steps")

BDF took 34 steps

The number of steps selected was reduced by a factor of 20!

11.3 Absolute stability¶

Example 11.3.5

Euler and Backward Euler time-stepping methods were used to solve $\mathbf{u}'=\mathbf{D}_{xx}\mathbf{u}$ .

m = 40
Dxx = FNC.diffper(m, [0, 1])[2]

The eigenvalues of this matrix are real and negative:

from scipy.linalg import eigvals
lamb = eigvals(Dxx)
plot(real(lamb), imag(lamb), "o")
xlabel("Re $\\lambda$")
ylabel("Im $\\lambda$")
title("Eigenvalues");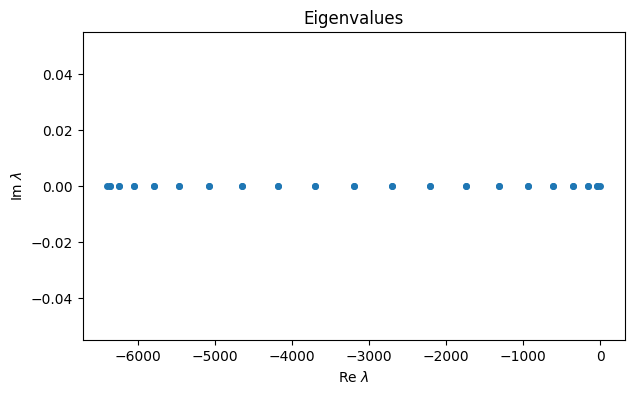

The Euler method is absolutely stable in the region $|\zeta+1| \le 1$ in the complex plane:

phi = 2 * pi * arange(361) / 360
z = exp(1j * phi) - 1  # unit circle shifted to the left by 1

fill(real(z), imag(z), color=(0.8, 0.8, 1))
xlabel("Re $\\lambda$")
ylabel("Im $\\lambda$")
axis("equal")
title("Stability region");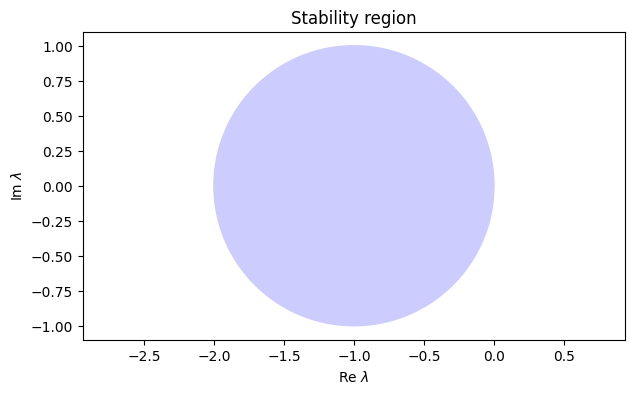

In order to get inside this region, we have to find τ such that $\lambda \tau > -2$ for all eigenvalues λ. This is an upper bound on τ.

lambda_min = min(real(lamb))
max_tau = -2 / lambda_min
print(f"predicted max time step is {max_tau:.3e}")

predicted max time step is 3.125e-04

Here we plot the resulting values of $\zeta=\lambda \tau$ .

zeta = lamb * max_tau
fill(real(z), imag(z), color=(0.8, 0.8, 1))
plot(real(zeta), imag(zeta), "o")
xlabel("Re $\\lambda$")
ylabel("Im $\\lambda$")
axis("equal")
title("Stability region and $\zeta$ values");

<>:7: SyntaxWarning: invalid escape sequence '\z'
<>:7: SyntaxWarning: invalid escape sequence '\z'
/var/folders/gc/0752xrm56pnf0r0dsrn5370c0000gr/T/ipykernel_93670/2266119891.py:7: SyntaxWarning: invalid escape sequence '\z'
  title("Stability region and $\zeta$ values");

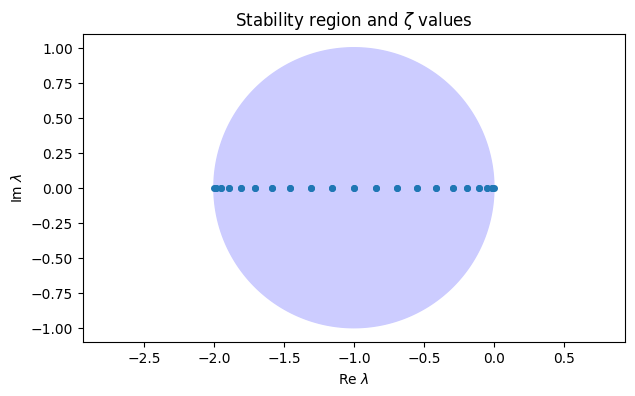
In backward Euler, the region is $|\zeta-1|\ge 1$ . Because they are all on the negative real axis, all of the ζ values will fit no matter what τ is chosen.

fill([-6, 6, 6, -6], [-6, -6, 6, 6], color=(0.8, 0.8, 1))
z = exp(1j * phi) + 1
# unit circle shifted right by 1
fill(real(z), imag(z), color="w")

plot(real(zeta), imag(zeta), "o")
axis([-4, 2, -3, 3])
axis("equal")
xlabel("Re $\\lambda$")
ylabel("Im $\\lambda$")
title("Stability region and $\\zeta$ values");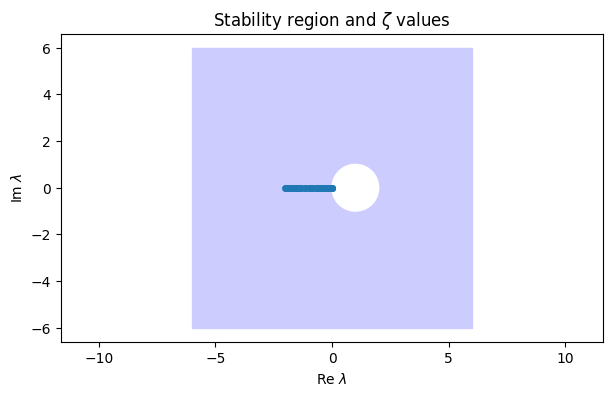

11.4 Stiffness¶

Example 11.4.2

In Example 11.4.1 we derived a Jacobian matrix for the Oregonator model. Here is a numerical solution of the ODE.

from scipy.integrate import solve_ivp
q, s, w = (8.375e-6, 77.27, 0.161)

def ode(t, u):
    return array(
        [
            s * (u[1] - u[0] * u[1] + u[0] - q * u[0]**2),
            (-u[1] - u[0] * u[1] + u[2]) / s,
            w * (u[0] - u[2]),
        ]
    )

u0 = array([1.0, 2.0, 3.0])
tspan = (0, 500)
start = timer()
sol = solve_ivp(ode, tspan, u0, method="BDF")
semilogy(sol.t, sol.y.T)
xlabel("$t$"),  ylabel("$u(t)$")
title("Oregonator");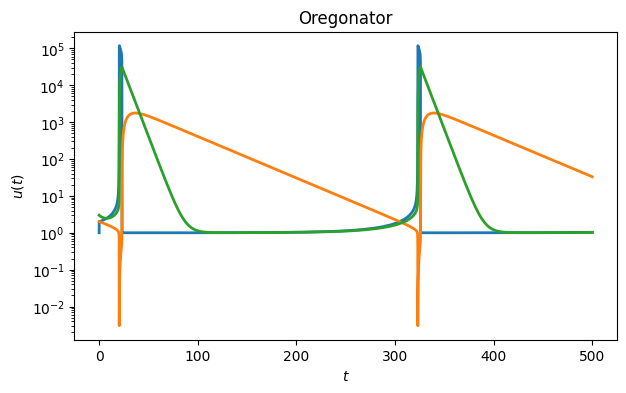

At each value of the numerical solution, we can compute the eigenvalues of the Jacobian. Here we plot all of those eigenvalues in the complex plane.

J = lambda u: array(
    [
        [-s * (u[1] + 1 - 2 * q * u[0]), s * (1 - u[0]), 0],
        [-u[1] / s, (-1 - u[0]) / s, 1 / s],
        [w, 0, -w],
    ]
)

from scipy.linalg import eigvals

lamb = array([eigvals(J(u)) for u in sol.y.T])
ax = figure().add_subplot(projection='3d')
for i in range(3):
    ax.plot(real(lamb[:, i]), imag(lamb[:, i]), sol.t, ".")
ax.set_xlabel("Re $\\lambda$")
ax.set_ylabel("Im $\\lambda$")
ax.set_zlabel("$t$")
ax.set_title("Oregonator eigenvalues");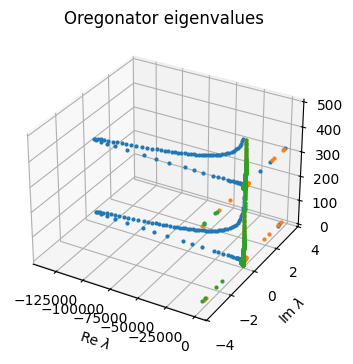

You can see that there is one eigenvalue that ranges over a wide portion of the negative real axis and dominates stability considerations.

Example 11.4.3

The BDF solver is good for stiff problems and needs few time steps to solve the Oregonator from Demo 11.4.2.

tspan = (0, 25)
start = timer()
sol = solve_ivp(ode, tspan, u0, method="BDF")
print(f"stiff solver took {timer() - start:.3f} seconds with {len(sol.t) - 1} time steps")

stiff solver took 0.093 seconds with 198 time steps

But if we apply Function 6.5.2 to the problem, the step size will be made small enough to cope with the large negative eigenvalue.

start = timer()
t, u = FNC.rk23(ode, tspan, u0, 1e-6)
print(f"rk23 solver took {timer() - start:.3f} seconds with {len(t) - 1} time steps")

rk23 solver took 3.771 seconds with 21388 time steps

Starting from the eigenvalues of the Jacobian matrix, we can find an effective $\zeta(t)$ by multiplying with the local time step size. The values of $\zeta(t)$ for each time level are plotted below and color coded by component of the diagonalized system.

zeta = zeros([len(t)- 1, 3]) + 0j    # complex array
for i in range(len(t) - 1):
    dt = t[i+1] - t[i]
    lamb = eigvals(J(u[:, i]))
    zeta[i] = lamb * dt
plot(real(zeta), imag(zeta), ".")
axis("equal")
xlabel("Re $\\zeta$")
ylabel("Im $\\zeta$")
title("Oregonator stability");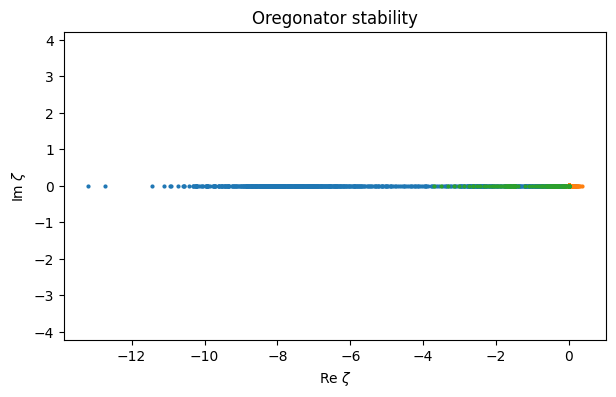

Roughly speaking, the ζ values stay within or close to the RK2 stability region in Figure 11.3.2. Momentary departures from the region are possible, but time stepping repeatedly in that situation would cause instability.

11.5 Boundaries¶

Example 11.5.3

First, we define functions for the PDE and each boundary condition.

phi = lambda t, x, u, ux, uxx: uxx
ga = lambda u, ux: u
gb = lambda u, ux: u - 2

Our next step is to write a function to define the initial condition. This one satisfies the boundary conditions exactly.

init = lambda x: 1 + sin(pi * x/2) + 3 * (1 - x**2) * exp(-4*x**2)

Now we can use Function 11.5.2 to solve the problem.

x, u = FNC.parabolic(phi, (-1, 1), 60, ga, gb, (0, 0.75), init)

for t in arange(0,0.5,0.1):
    plot(x, u(t), label=f"t={t:.2f}")
xlabel("$x$"),  ylabel("$u(x,t)$")
legend()
title("Heat equation with Dirichlet boundaries");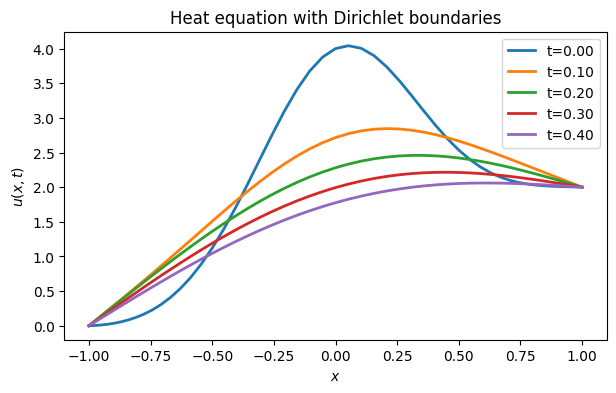

from matplotlib import animation
fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(-1, 1), ylim=(0, 4.2))

line, = ax.plot([], [], '-')
ax.set_title("Heat equation with Dirichlet boundaries")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

def animate(t):
    line.set_data(x, u(t))
    time_text.set_text(f"t = {t:.2e}")
    return line, time_text

anim = animation.FuncAnimation(
    fig, animate, frames=linspace(0, 0.75, 201), blit=True)
anim.save("figures/boundaries-heat.mp4", fps=30)
close()

Example 11.5.4

phi = lambda t, x, u, ux, uxx: u**2 + uxx
ga = lambda u, ux: u
gb = lambda u, ux: ux
init = lambda x: 400 * x**4 * (1 - x)**2
x, u = FNC.parabolic(phi, (0, 1), 60, ga, gb, (0, 0.1), init);

fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, 1), ylim=(0, 10))

line, = ax.plot([], [], '-')
ax.set_title("Heat equation with source")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

anim = animation.FuncAnimation(
    fig, animate, frames=linspace(0, 0.1, 101), blit=True)
anim.save("figures/boundaries-source.mp4", fps=30)
close()

Example 11.5.5

K = 3;  sigma = 0.06;  r = 0.08;  Smax = 8;
phi = lambda t, x, u, ux, uxx: sigma**2/2 * (x**2 * uxx) + r*x*ux - r*u
ga = lambda u, ux: u
gb = lambda u, ux: ux - 1

u0 = lambda x: maximum(0, x - K)
x, u = FNC.parabolic(phi, (0, Smax), 80, ga, gb, (0, 15), u0);

fig = figure()
ax = fig.add_subplot(autoscale_on=False, xlim=(0, Smax), ylim=(-0.5, 8))

line, = ax.plot([], [], '-')
ax.set_title("Black–Scholes equation with boundaries")
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

anim = animation.FuncAnimation(
    fig, animate, frames=linspace(0, 15, 151), blit=True)
anim.save("figures/boundaries-bs.mp4", fps=30)
close()

Recall that $u$ is the value of the call option, and time runs backward from the strike time. The longer the horizon, the more value the option has due to anticipated growth in the stock price.