Functions¶
Hat function
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23function H = hatfun(t, k) % HATFUN Hat function/piecewise linear basis function. % Input: % t interpolation nodes (vector, length n+1) % k node index (integer, in 0,...,n) % Output: % H kth hat function (function) n = length(t) - 1; function y = evaluate(x) y = zeros(size(x)); for i = 1:numel(x) if (k > 0) && (t(k) <= x(i)) && (x(i) <= t(k+1)) y(i) = (x(i) - t(k)) / (t(k+1) - t(k)); elseif (k < n) && (t(k+1) <= x(i)) && (x(i) <= t(k+2)) y(i) = (t(k+2) - x(i)) / (t(k+2) - t(k+1)); end end end H = @evaluate; end
Piecewise linear interpolation
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24function p = plinterp(t,y) % PLINTERP Piecewise linear interpolation. % Input: % t interpolation nodes (vector, length n+1) % y interpolation values (vector, length n+1) % Output: % p piecewise linear interpolant (function) n = length(t) - 1; H = {}; for k = 0:n H{k+1} = hatfun(t, k); end p = @evaluate; % This function evaluates p when called. function f = evaluate(x) f = 0; for k = 0:n f = f + y(k+1) * H{k+1}(x); end end end
Cubic spline interpolation
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60function S = spinterp(t,y) % SPINTERP Cubic not-a-knot spline interpolation. % Input: % t interpolation nodes (vector, length n+1) % y interpolation values (vector, length n+1) % Output: % S not-a-knot cubic spline (function) t = t(:); y = y(:); % ensure column vectors n = length(t)-1; h = diff(t); % differences of all adjacent pairs % Preliminary definitions. Z = zeros(n); I = eye(n); E = I(1:n-1,:); J = I - diag(ones(n-1,1),1); H = diag(h); % Left endpoint interpolation: AL = [ I, Z, Z, Z ]; vL = y(1:n); % Right endpoint interpolation: AR = [ I, H, H^2, H^3 ]; vR = y(2:n+1); % Continuity of first derivative: A1 = E*[ Z, J, 2*H, 3*H^2 ]; v1 = zeros(n-1,1); % Continuity of second derivative: A2 = E*[ Z, Z, J, 3*H ]; v2 = zeros(n-1,1); % Not-a-knot conditions: nakL = [ zeros(1,3*n), [1,-1, zeros(1,n-2)] ]; nakR = [ zeros(1,3*n), [zeros(1,n-2), 1,-1] ]; % Assemble and solve the full system. A = [ AL; AR; A1; A2; nakL; nakR ]; v = [ vL; vR; v1; v2; 0 ;0 ]; z = A\v; % Break the coefficients into separate vectors. rows = 1:n; a = z(rows); b = z(n+rows); c = z(2*n+rows); d = z(3*n+rows); S = @evaulate; % This function evaluates the spline when called with a value for x. function f = evaulate(x) f = zeros(size(x)); for k = 1:n % iterate over the pieces % Evalaute this piece's cubic at the points inside it. index = (x>=t(k)) & (x<=t(k+1)); f(index) = polyval( [d(k),c(k),b(k),a(k)], x(index)-t(k) ); end end end
Fornberg’s algorithm for finite difference weights
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40function w = fdweights(t,m) %FDWEIGHTS Fornberg's algorithm for finite difference weights. % Input: % t nodes (vector, length r+1) % m order of derivative sought at x=0 (integer scalar) % Output: % w weights for the approximation to the jth derivative (vector) % This is a compact implementation, not an efficient one. r = length(t)-1; w = zeros(size(t)); for k = 0:r w(k+1) = weight(t,m,r,k); end function c = weight(t,m,r,k) % Implement a recursion for the weights. % Input: % t nodes (vector) % m order of derivative sought % r number of nodes to use from t (<= length(t)) % k index of node whose weight is found % Output: % c finite difference weight if (m<0) || (m>r) % undefined coeffs must be zero c = 0; elseif (m==0) && (r==0) % base case of one-point interpolation c = 1; else % generic recursion if k<r c = (t(r+1)*weight(t,m,r-1,k) - ... m*weight(t,m-1,r-1,k))/(t(r+1)-t(k+1)); else beta = prod(t(r)-t(1:r-1)) / prod(t(r+1)-t(1:r)); c = beta*(m*weight(t,m-1,r-1,r-1) - t(r)*weight(t,m,r-1,r-1)); end end
Trapezoid formula for numerical integration
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15function [T,t,y] = trapezoid(f,a,b,n) %TRAPEZOID Trapezoid formula for numerical integration. % Input: % f integrand (function) % a,b interval of integration (scalars) % n number of interval divisions % Output: % T approximation to the integral of f over (a,b) % t vector of nodes used % y vector of function values at nodes h = (b-a)/n; t = a + h*(0:n)'; y = f(t); T = h * ( sum(y(2:n)) + 0.5*(y(1) + y(n+1)) );
Adaptive integration
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42function [Q,t] = intadapt(f,a,b,tol) %INTADAPT Adaptive integration with error estimation. % Input: % f integrand (function) % a,b interval of integration (scalars) % tol acceptable error % Output: % Q approximation to integral(f,a,b) % t vector of nodes used m = (b+a)/2; [Q,t] = do_integral(a,f(a),b,f(b),m,f(m),tol); % Use error estimation and recursive bisection. function [Q,t] = do_integral(a,fa,b,fb,m,fm,tol) % These are the two new nodes and their f-values. xl = (a+m)/2; fl = f(xl); xr = (m+b)/2; fr = f(xr); t = [a;xl;m;xr;b]; % all 5 nodes at this level % Compute the trapezoid values iteratively. h = (b-a); T(1) = h*(fa+fb)/2; T(2) = T(1)/2 + (h/2)*fm; T(3) = T(2)/2 + (h/4)*(fl+fr); S = (4*T(2:3)-T(1:2)) / 3; % Simpson values E = (S(2)-S(1)) / 15; % error estimate if abs(E) < tol*(1+abs(S(2))) % acceptable error? Q = S(2); % yes--done else % Error is too large--bisect and recurse. [QL,tL] = do_integral(a,fa,m,fm,xl,fl,tol); [QR,tR] = do_integral(m,fm,b,fb,xr,fr,tol); Q = QL + QR; t = [tL;tR(2:end)]; % merge the nodes w/o duplicate end end end % main function
About the code
The intended way for a user to call Function 5.7.1 is with only f, a, b, and tol provided. We then use default values on the other parameters to compute the function values at the endpoints, the interval’s midpoint, and the function value at the midpoint. Recursive calls from within the function itself will provide all of that information, since it was already calculated along the way.
Examples¶
5.1 The interpolation problem¶
Example 5.1.1
Here are some points that we could consider to be observations of an unknown function on .
n = 5;
t = linspace(-1,1,n+1)';
y = t.^2 + t + 0.05 * sin(20 * t);
clf, scatter(t,y)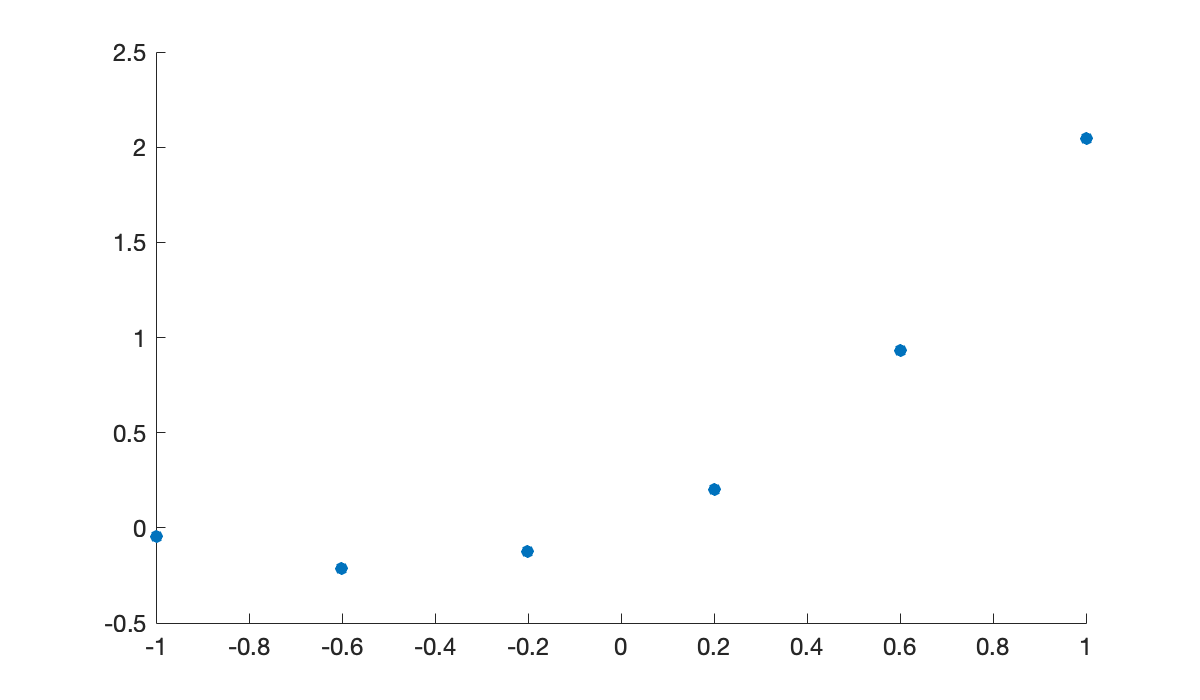
The polynomial interpolant, as computed using polyfit, looks very sensible. It’s the kind of function you’d take home to meet your parents.
c = polyfit(t, y, n); % polynomial coefficients
p = @(x) polyval(c, x);
hold on
fplot(p, [-1 1])
legend('data', 'interpolant', 'location', 'north');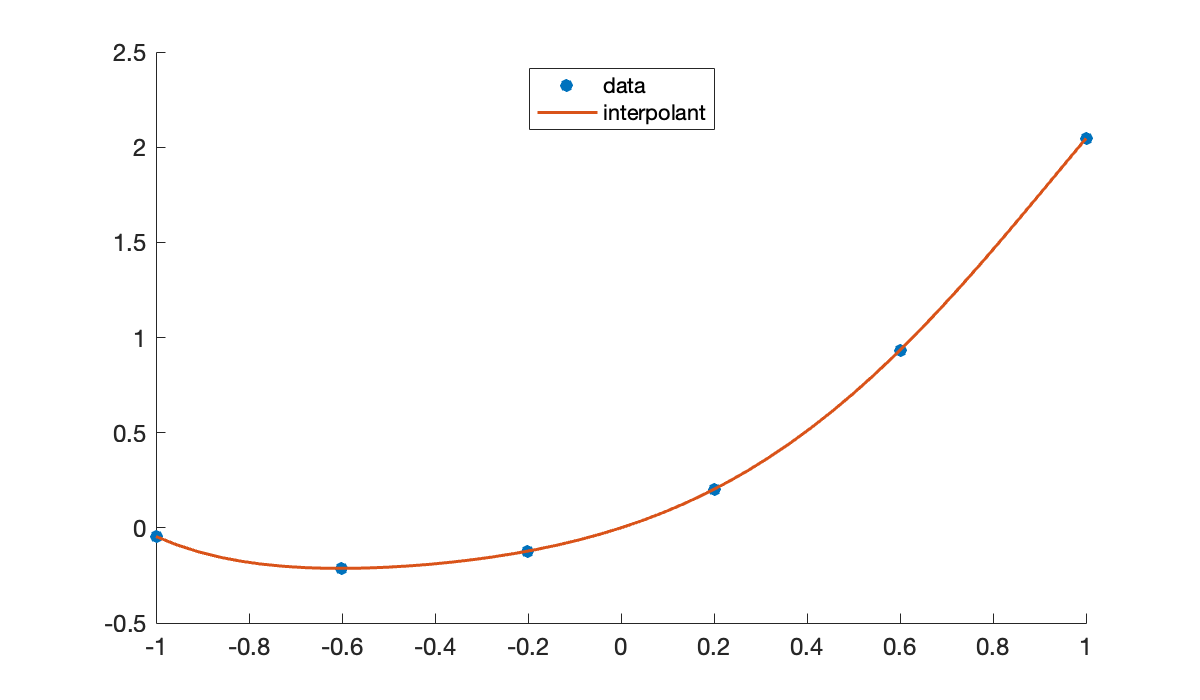
But now consider a different set of points generated in almost exactly the same way.
n = 18;
t = linspace(-1, 1, n+1);
y = t.^2 + t + 0.05 * sin(20 * t);
clf, scatter(t, y)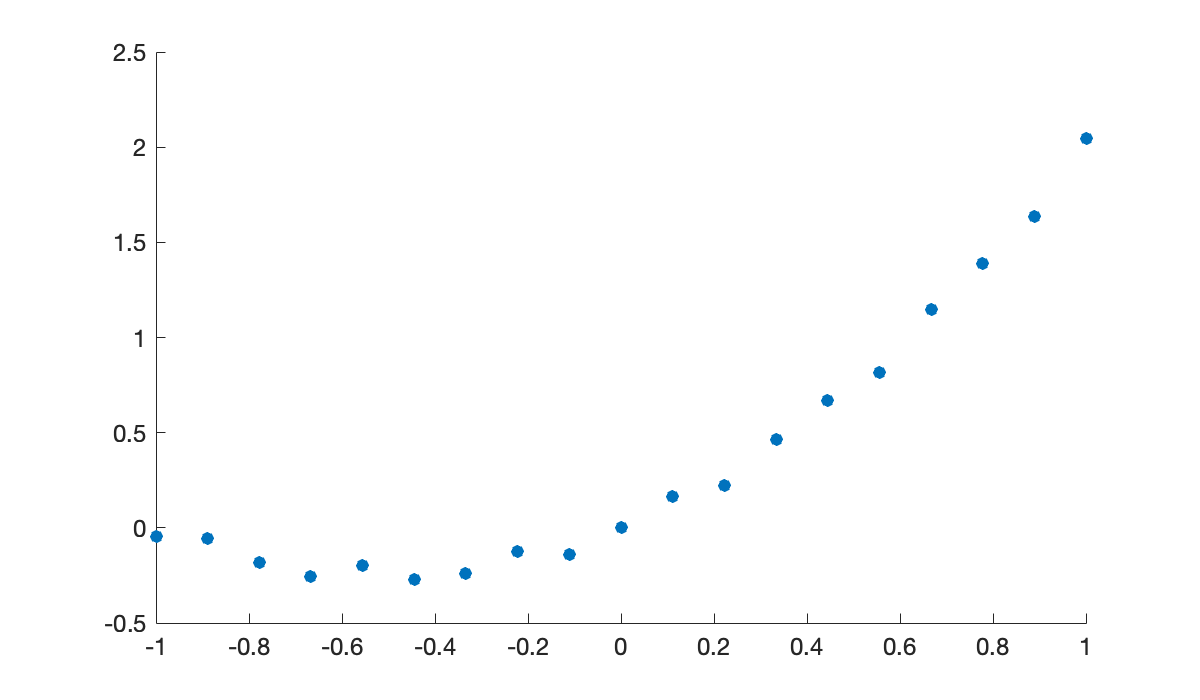
The points themselves are unremarkable. But take a look at what happens to the polynomial interpolant.
c = polyfit(t, y, n); % polynomial coefficients
p = @(x) polyval(c, x);
hold on, fplot(p, [-1 1])
legend('data', 'interpolant', 'location', 'north');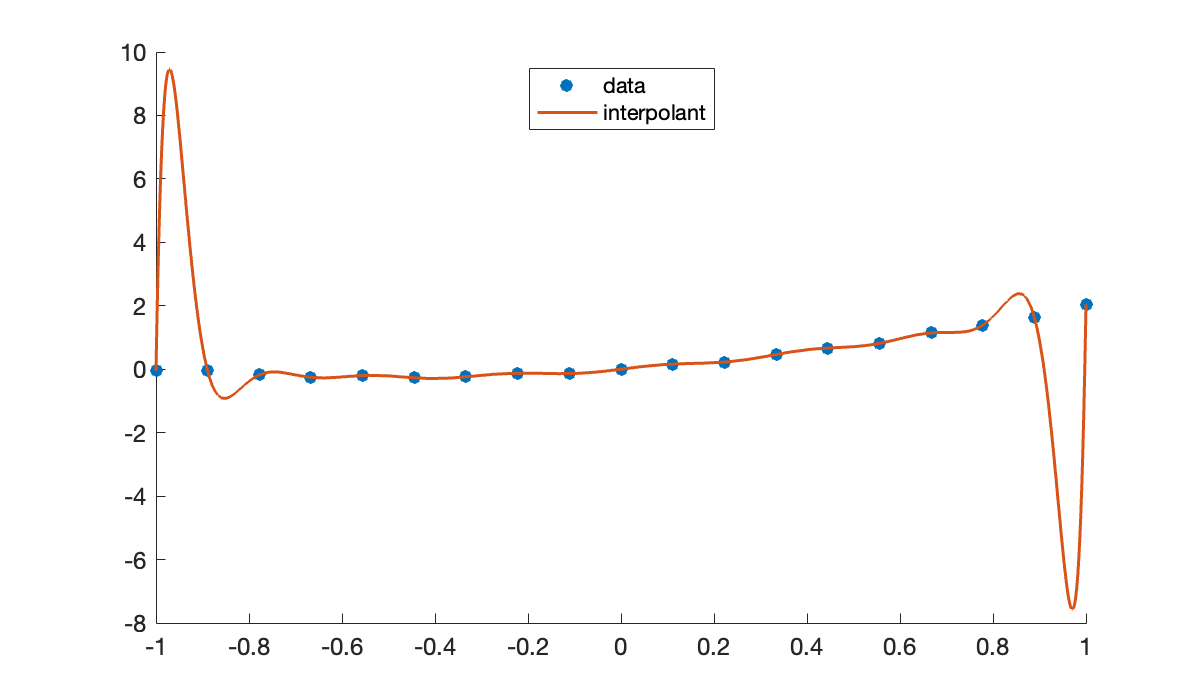
Surely there must be functions that are more intuitively representative of those points!
Example 5.1.3
Let us recall the data from Demo 5.1.1.
n = 18;
t = linspace(-1, 1, n+1);
y = t.^2 + t + 0.05 * sin(20 * t);
clf, scatter(t, y)
Here is an interpolant that is linear between each consecutive pair of nodes, using interp1 from MATLAB.
x = linspace(-1, 1, 400)';
hold on, plot(x, interp1(t, y, x))
title('Piecewise linear interpolant')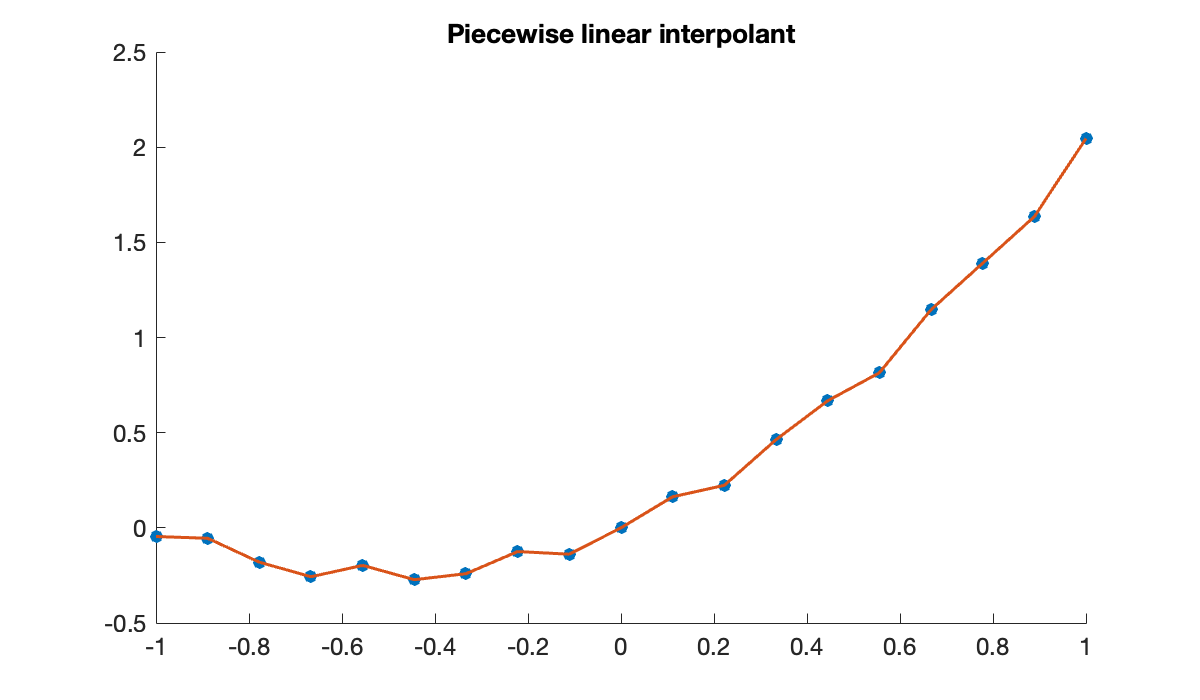
We may prefer a smoother interpolant that is piecewise cubic, generated using Spline1D from the Dierckx package.
cla
scatter(t, y)
plot(x, interp1(t, y, x, 'spline'))
title('Piecewise cubic interpolant')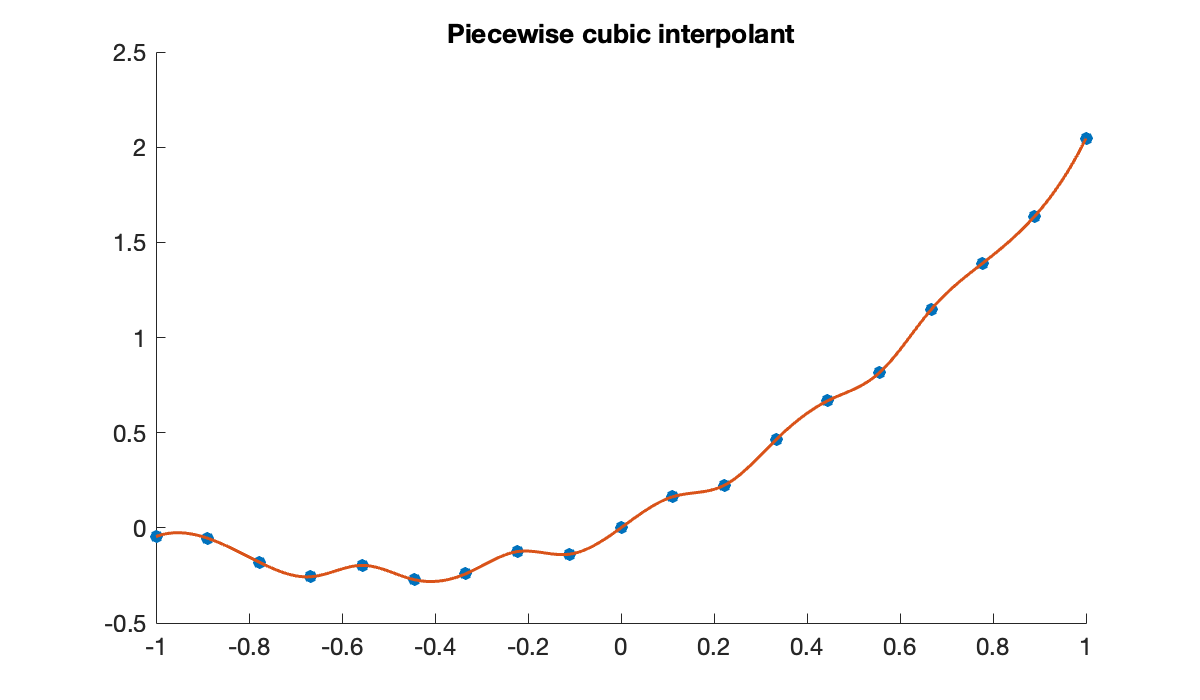
Example 5.1.4
In Demo 5.1.1 and Demo 5.1.3 we saw a big difference between polynomial interpolation and piecewise polynomial interpolation of some arbitrarily chosen data. The same effects can be seen clearly in the cardinal functions, which are closely tied to the condition numbers.
n = 18;
t = linspace(-1, 1, n+1)';
y = [zeros(9, 1); 1; zeros(n - 9, 1)]; % 10th cardinal function
clf, scatter(t, y)
hold on
x = linspace(-1, 1, 400)';
plot(x, interp1(t, y, x, 'spline'))
title('Piecewise cubic cardinal function')
xlabel('x'), ylabel('p(x)')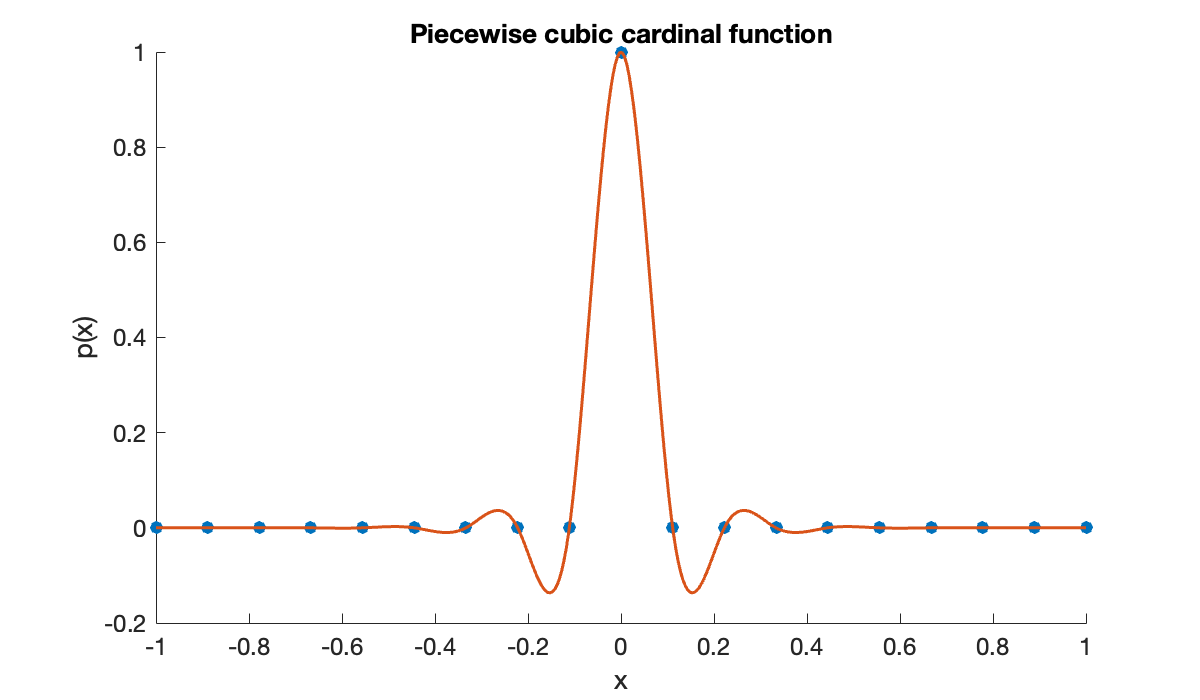
The piecewise cubic cardinal function is nowhere greater than one in absolute value. This happens to be true for all the cardinal functions, ensuring a good condition number for any interpolation with these functions. But the story for global polynomials is very different.
clf, scatter(t, y)
c = polyfit(t, y, n);
hold on, plot(x, polyval(c, x))
title('Polynomial cardinal function')
xlabel('x'), ylabel(('p(x)'));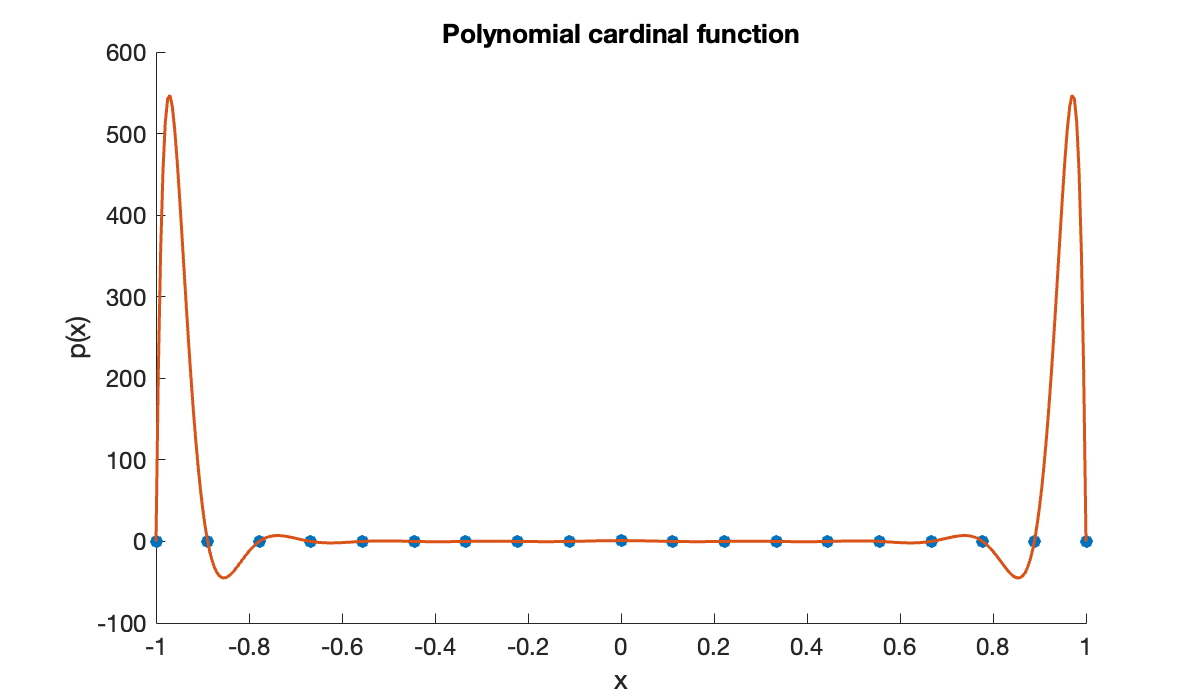
From the figure we can see that the condition number for polynomial interpolation on these nodes is at least 500.
5.2 Piecewise linear interpolation¶
Example 5.2.1
Let’s define a set of four nodes (i.e., in our formulas).
t = [0, 0.55, 0.7, 1];We plot the hat functions .
clf
for k = 0:3
subplot(4, 1, k+1)
Hk = hatfun(t, k);
fplot(Hk, [0, 1])
hold on
scatter(t, Hk(t))
text(t(k+1), 0.6, sprintf("H_%d", k))
end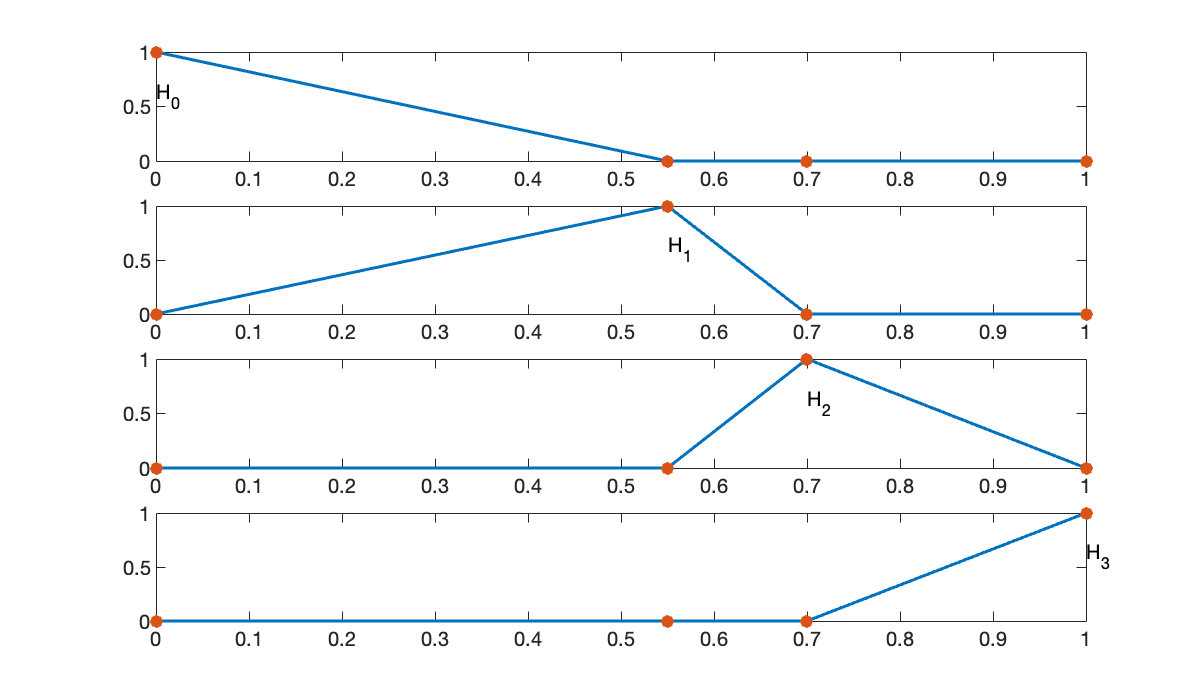
Example 5.2.2
We generate a piecewise linear interpolant of .
f = @(x) exp(sin(7 * x));
clf
fplot(f, [0, 1], displayname="function")
xlabel("x"); ylabel(("y"));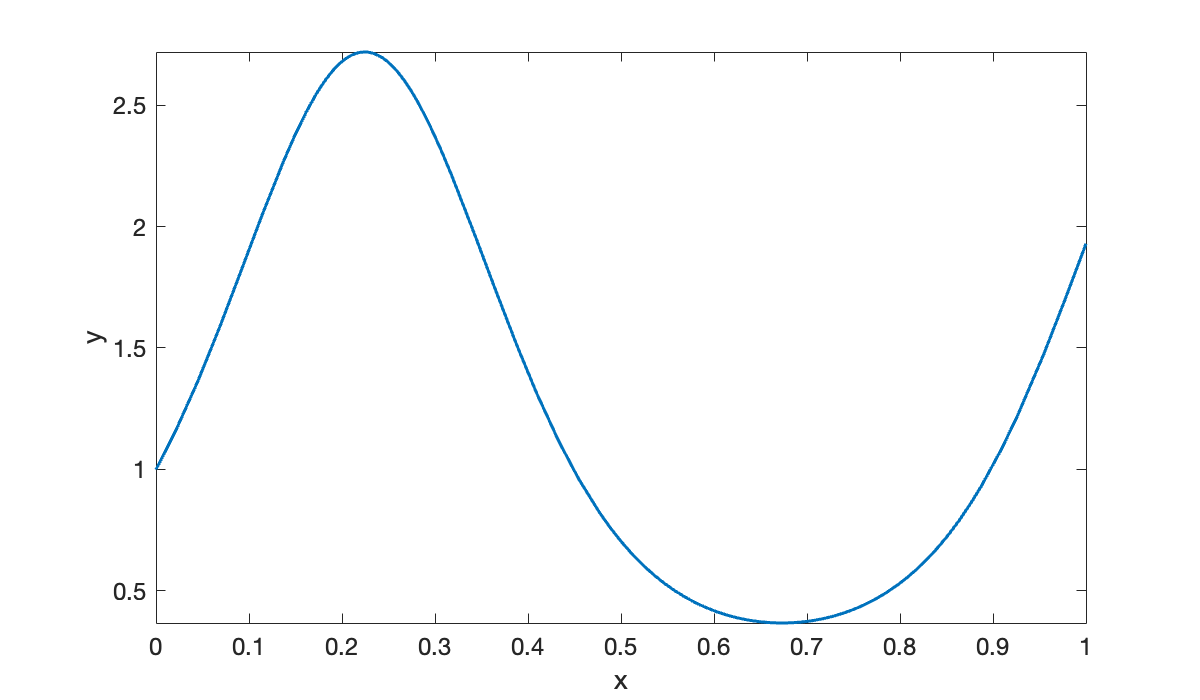
First we sample the function to create the data.
t = [0, 0.075, 0.25, 0.55, 0.7, 1]; % nodes
y = f(t); % function valuesNow we create a callable function that will evaluate the piecewise linear interpolant at any , and then plot it.
p = plinterp(t, y);
hold on
fplot(p, [0, 1], displayname="interpolant")
scatter(t, y, displayname="values at nodes")
title("PL interpolation")
legend();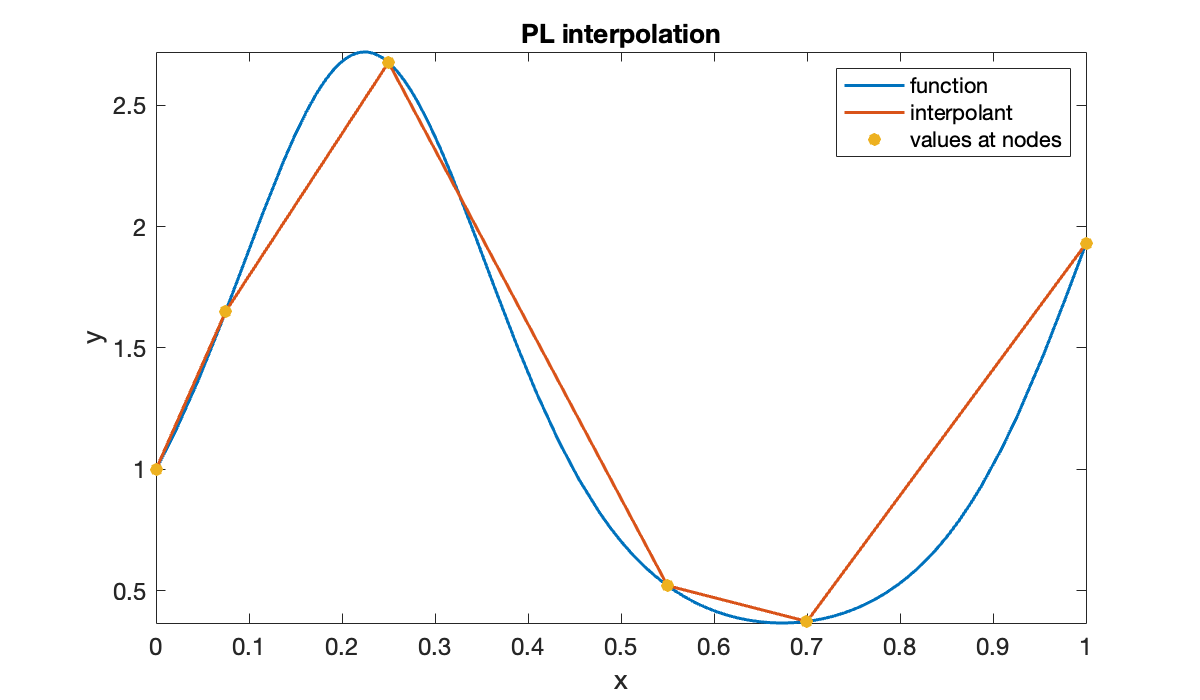
Example 5.2.3
We measure the convergence rate for piecewise linear interpolation of over .
f = @(x) exp(sin(7 * x));
x = linspace(0, 1, 10001)'; % sample the difference at many points
n = round(10.^(1:0.25:3.5))';
maxerr = zeros(size(n));
for i = 1:length(n)
t = (0:n(i)) / n(i); % interpolation nodes
p = plinterp(t, f(t));
maxerr(i) = norm(f(x) - p(x), Inf);
end
table(n(1:4:end), maxerr(1:4:end), variableNames=["n", "inf-norm error"])As predicted, a factor of 10 in produces a factor of 100 reduction in the error. In a convergence plot, it is traditional to have decrease from left to right, so we expect a straight line of slope -2 on a log-log plot.
clf
loglog(n, maxerr, "-o", displayname="error")
order2 = 0.5 * maxerr(end) * (n / n(end)) .^ (-2);
hold on
loglog(n, order2, "k--", displayname="O(n^{-2})")
xlabel("n"); ylabel("|| f-p ||_{\infty}")
title("Convergence of PL interpolation")
legend();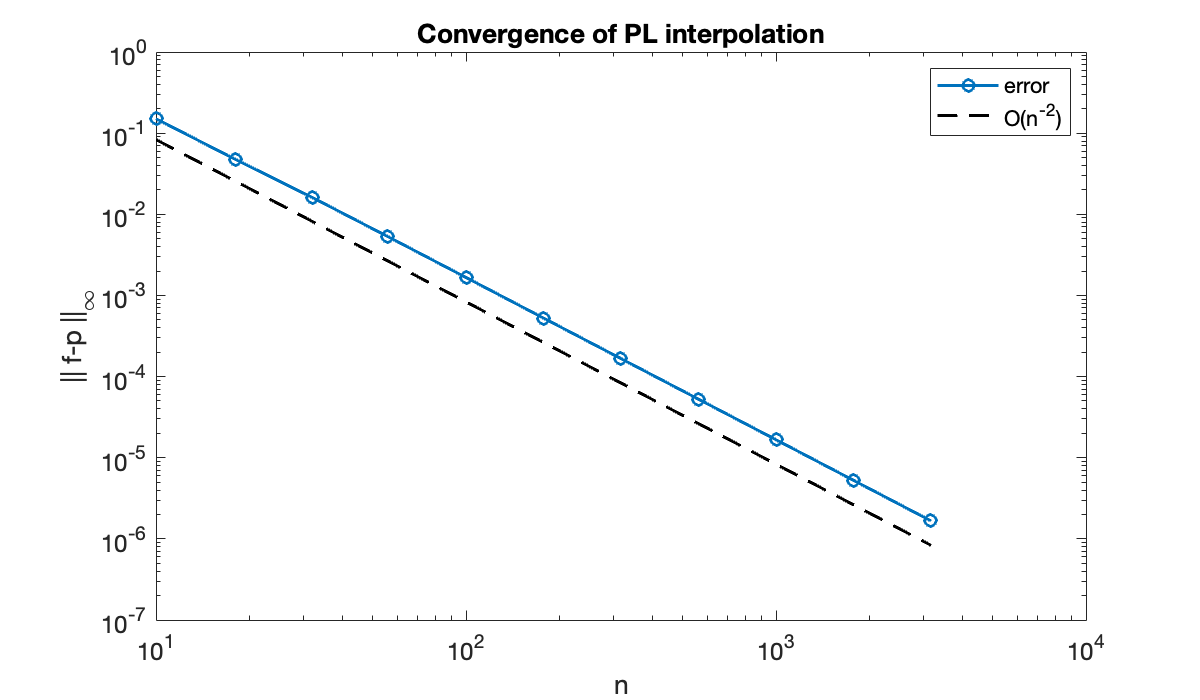
5.3 Cubic splines¶
Example 5.3.1
For illustration, here is a spline interpolant using just a few nodes.
clf
f = @(x) exp(sin(7 * x));
fplot(f, [0, 1], displayname="function")
t = [0, 0.075, 0.25, 0.55, 0.7, 1]; % nodes
y = f(t); % values at nodes
hold on, scatter(t, y, displayname="values at nodes")
S = spinterp(t, y);
fplot(S, [0, 1], displayname="spline")
xlabel("x"); ylabel("y")
legend();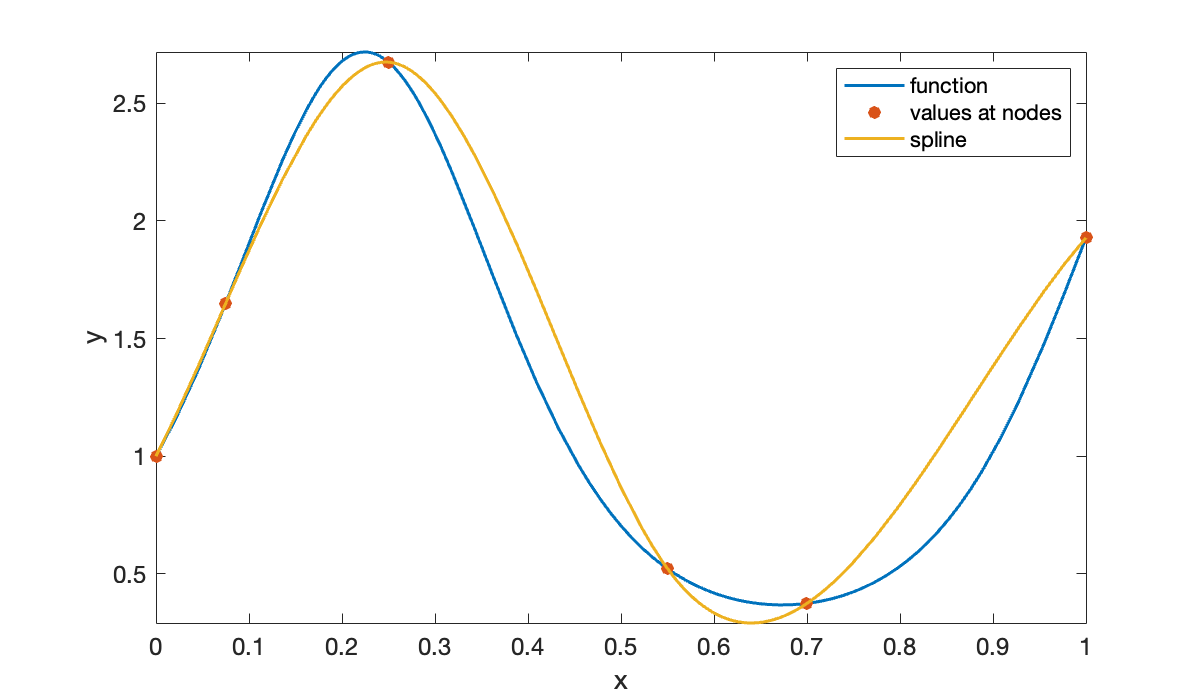
Now we look at the convergence rate as the number of nodes increases.
x = (0:10000)' / 1e4; % sample the difference at many points
n = round(2 .^ (3:0.5:7))'; % numbers of nodes
maxerr = zeros(size(n));
for i = 1:length(n)
t = (0:n(i))' / n(i);
S = spinterp(t, f(t));
err = f(x) - S(x);
maxerr(i) = norm(err, Inf);
end
table(n(1:2:end), maxerr(1:2:end), variableNames=["n", "inf-norm error"])Since we expect convergence that is , we use a log-log graph of error and expect a straight line of slope -4.
clf
loglog(n, maxerr, "-o", displayname="error")
order4 = 0.5 * maxerr(end) * (n / n(end)) .^ (-4);
hold on
loglog(n, order4, "k--", displayname="O(n^{-4})")
xlabel("n"); ylabel("|| f-S ||_{\infty}")
title(("Convergence of spline interpolation"));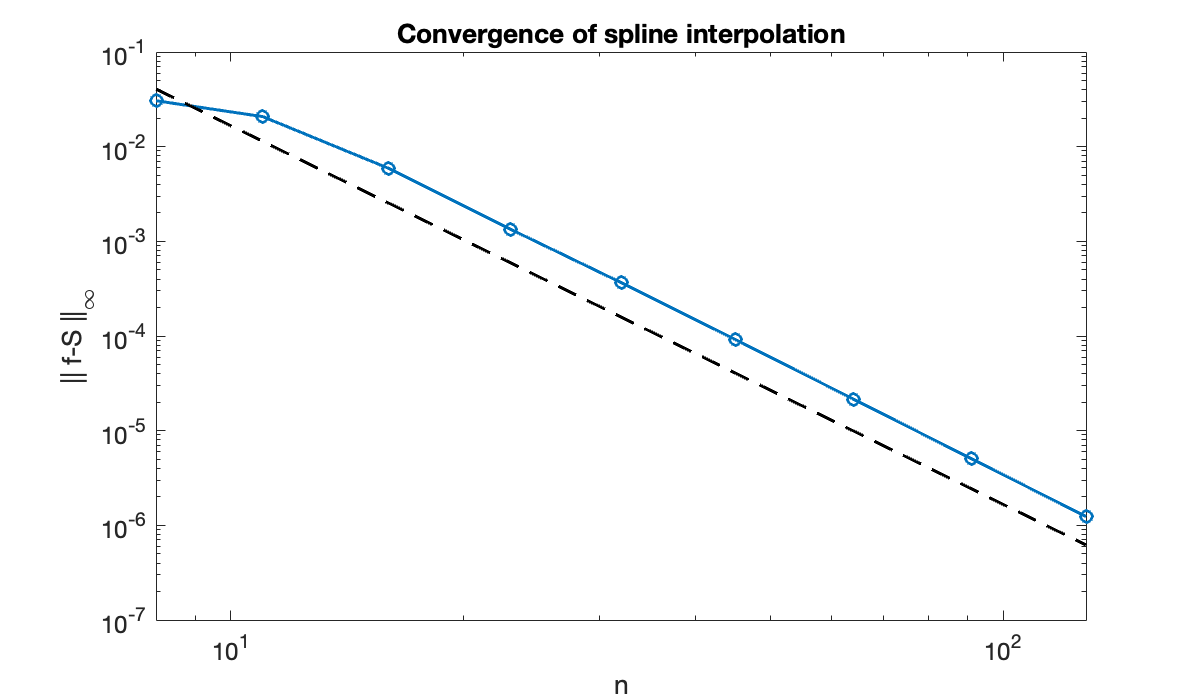
5.4 Finite differences¶
Example 5.4.3
If , then .
f = @(x) exp(sin(x));Here are the first two centered differences from Table 5.4.1.
h = 0.05;
format long
CD2 = (-f(-h) + f(h)) / (2*h)
CD4 = (f(-2*h) - 8*f(-h) + 8*f(h) - f(2*h)) / (12*h)Here are the first two forward differences from Table 5.4.2.
FD1 = (-f(0) + f(h)) / h
FD2 = (-3*f(0) + 4*f(h) - f(2*h)) / (2*h)Finally, here are the backward differences that come from reverse-negating the forward differences.
BD1 = (-f(-h) + f(0)) / h
BD2 = (f(-2*h) - 4*f(-h) + 3*f(0)) / (2*h)Example 5.4.4
If , then .
f = @(x) exp(sin(x));Here is a centered estimate given by (5.4.12).
h = 0.05;
format long
CD2 = (f(-h) - 2*f(0) + f(h)) / h^2For the same , here are forward estimates given by (5.4.13) and (5.4.14).
FD1 = (f(0) - 2*f(h) + f(2*h)) / h^2
FD2 = (2*f(0) - 5*f(h) + 4*f(2*h) - f(3*h)) / h^2Finally, here are the backward estimates that come from reversing (5.4.13) and (5.4.14).
BD1 = (f(-2*h) - 2*f(-h) + f(0)) / h^2
BD2 = (-f(-3*h) + 4*f(-2*h) - 5*f(-h) + 2*f(0)) / h^2Example 5.4.5
We will estimate the derivative of at using five nodes.
t = [0.35, 0.5, 0.57, 0.6, 0.75]; % nodes
f = @(x) cos(x.^2);
dfdx = @(x) -2 * x * sin(x^2);
exact_value = dfdx(0.5)We have to shift the nodes so that the point of estimation for the derivative is at . (To subtract a scalar from a vector, we must use the .- operator.)
format short
w = fdweights(t - 0.5, 1)The finite-difference formula is a dot product (i.e., inner product) between the vector of weights and the vector of function values at the nodes.
fd_value = w * f(t)'We can reproduce the weights in the finite-difference tables by using equally spaced nodes with . For example, here is a one-sided formula at four nodes.
fdweights(0:3, 1)5.5 Convergence of finite differences¶
Example 5.5.3
Let’s observe the convergence of the formulas in Example 5.5.1 and Example 5.5.2, applied to the function at .
f = @(x) sin(exp(x + 1));
exact_value = exp(1) * cos(exp(1))We’ll compute the formulas in parallel for a sequence of values.
h = 5 ./ 10.^(1:6)';
FD1 = zeros(size(h));
FD2 = zeros(size(h));
for i = 1:length(h)
h_i = h(i);
FD1(i) = (f(h_i) - f(0) ) / h_i;
FD2(i) = (f(h_i) - f(-h_i)) / (2*h_i);
end
table(h, FD1, FD2)All that’s easy to see from this table is that FD2 appears to converge to the same result as FD1, but more rapidly. A table of errors is more informative.
err1 = abs(exact_value - FD1);
err2 = abs(exact_value - FD2);
table(h, err1, err2, variableNames=["h", "error in FD1", "error in FD2"])In each row, is decreased by a factor of 10, so that the error is reduced by a factor of 10 in the first-order method and 100 in the second-order method.
A graphical comparison can be useful as well. On a log-log scale, the error should (as ) be a straight line whose slope is the order of accuracy. However, it’s conventional in convergence plots to show decreasing from left to right, which negates the slopes.
clf
loglog(h, abs([err1 err2]), "o-")
set(gca, "xdir", "reverse")
order1 = 0.1 * err1(end) * (h / h(end)) .^ 1;
order2 = 0.1 * err2(end) * (h / h(end)) .^ 2;
hold on
loglog(h, order1, "--", h, order2, "--")
xlabel("h"); ylabel("error")
title("Convergence of finite differences")
legend("FD1", "FD2", "O(h)", "O(h^2)");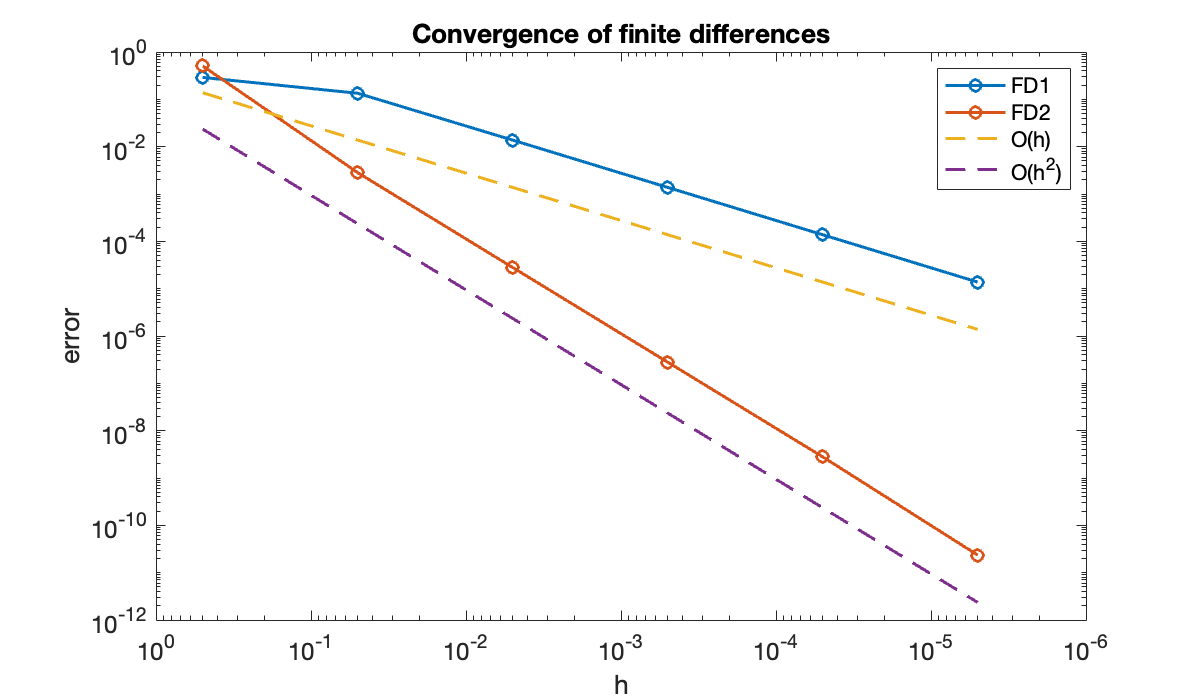
Example 5.5.4
Let . We apply finite-difference formulas of first, second, and fourth order to estimate .
f = @(x) exp(-1.3 * x);
exact = -1.3;
h = 10 .^ (-(1:12))';
FD = zeros(length(h), 3);
for i = 1:length(h)
h_i = h(i);
nodes = h_i * (-2:2);
vals = f(nodes);
FD(i, 1) = dot([0 0 -1 1 0] / h_i, vals);
FD(i, 2) = dot([0 -1/2 0 1/2 0] / h_i, vals);
FD(i, 3) = dot([1/12 -2/3 0 2/3 -1/12] / h_i, vals);
end
format long
table(h, FD(:, 1), FD(:, 2), FD(:, 3), variableNames=["h", "FD1", "FD2", "FD4"])They all seem to be converging to -1.3. The convergence plot reveals some interesting structure to the errors, though.
err = abs(FD - exact);
clf
loglog(h, err, "o-")
set(gca, "xdir", "reverse")
order1 = 0.1 * err(end, 1) * (h / h(end)) .^ (-1);
hold on
loglog(h, order1, "k--")
xlabel("h"); ylabel("error")
title("FD error with roundoff")
legend("FD1", "FD2", "FD4", "O(1/h)", "location", "northeast");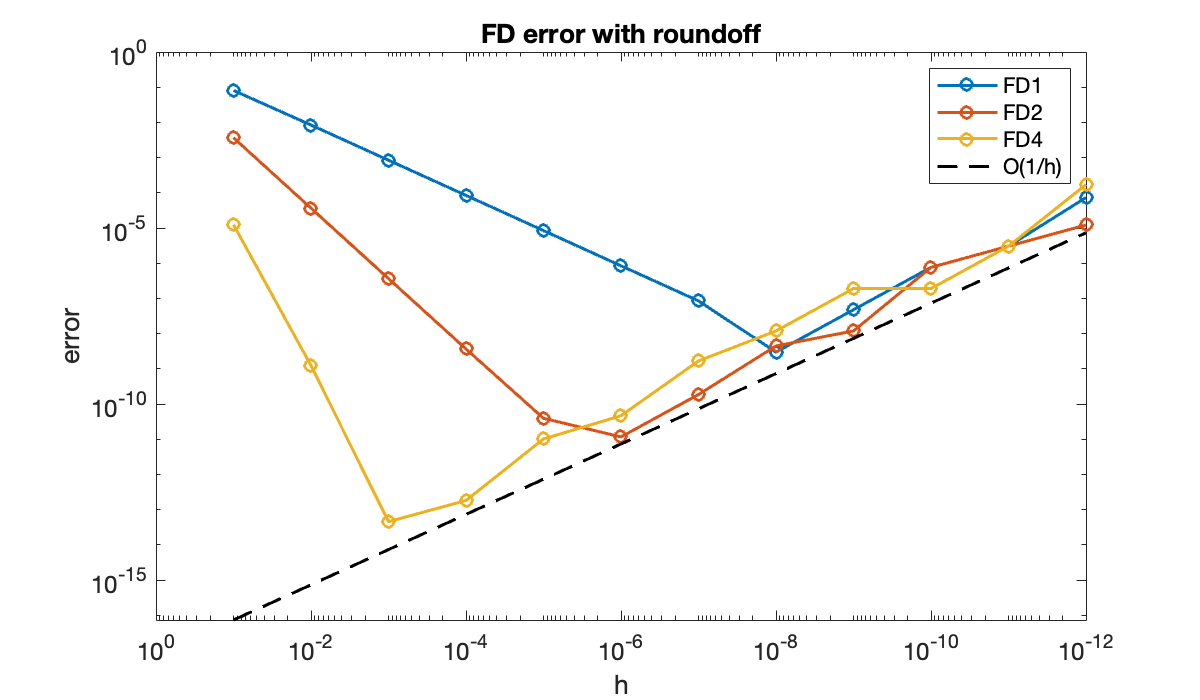
Again the graph is made so that decreases from left to right. The errors are dominated at first by truncation error, which decreases most rapidly for the fourth-order formula. However, increasing roundoff error eventually equals and then dominates the truncation error as continues to decrease. As the order of accuracy increases, the crossover point moves to the left (greater efficiency) and down (greater accuracy).
5.6 Numerical integration¶
Example 5.6.1
The antiderivative of is, of course, itself. That makes evaluation of by the Fundamental Theorem trivial.
format long
exact = exp(1) - 1MATLAB has numerical integrator integral that estimates the value without finding the antiderivative first. As you can see here, it can be as accurate as floating-point precision allows.
integral(@(x) exp(x), 0, 1)The numerical approach is also far more robust. For example, has no useful antiderivative. But numerically, it’s no more difficult.
integral(@(x) exp(sin(x)), 0, 1)When you look at the graphs of these functions, what’s remarkable is that one of these areas is basic calculus while the other is almost impenetrable analytically. From a numerical standpoint, they are practically the same problem.
x = linspace(0, 1, 201)';
subplot(2,1,1), fill([x; 1; 0], [exp(x); 0;0 ], [1, 0.9, 0.9])
title('exp(x)')
ylabel('f(x)')
subplot(2, 1, 2), fill([x; 1; 0], [exp(sin(x)); 0; 0], [1, 0.9, 0.9])
title('exp(sin(x))')
xlabel('x'), ylabel(('f(x)'));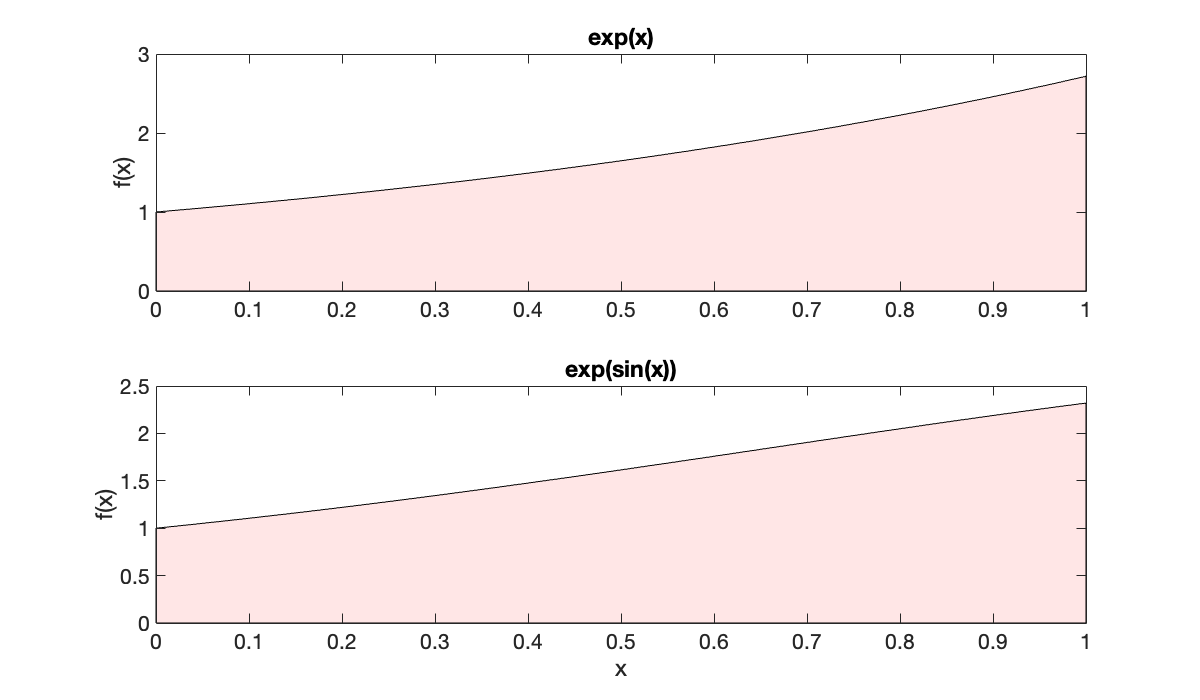
Example 5.6.2
We will approximate the integral of the function over the interval .
f = @(x) exp(sin(7 * x));
a = 0; b = 2;In lieu of the exact value, we use the integral function to find an accurate result.
I = integral(f, a, b, abstol=1e-14, reltol=1e-14);
fprintf("Integral = %.15f", I)Integral = 2.663219782761539Here is the trapezoid result at , and its error.
T = trapezoid(f, a, b, 40);
fprintf("Trapezoid error = %.2e", I - T)Trapezoid error = 9.17e-04In order to check the order of accuracy, we increase by orders of magnitude and observe how the error decreases.
n = 10 .^ (1:5)';
err = zeros(size(n));
for i = 1:length(n)
T = trapezoid(f, a, b, n(i));
err(i) = I - T;
end
table(n, err, variableNames=["n", "Trapezoid error"])Each increase by a factor of 10 in cuts the error by a factor of about 100, which is consistent with second-order convergence. Another check is that a log-log graph should give a line of slope -2 as .
clf
loglog(n, abs(err), "-o", displayname="trapezoid")
hold on
loglog(n, 0.1 * abs(err(end)) * (n / n(end)).^(-2), "k--", displayname="O(n^{-2})")
xlabel("n"); ylabel("error")
title("Convergence of trapezoidal integration")
legend();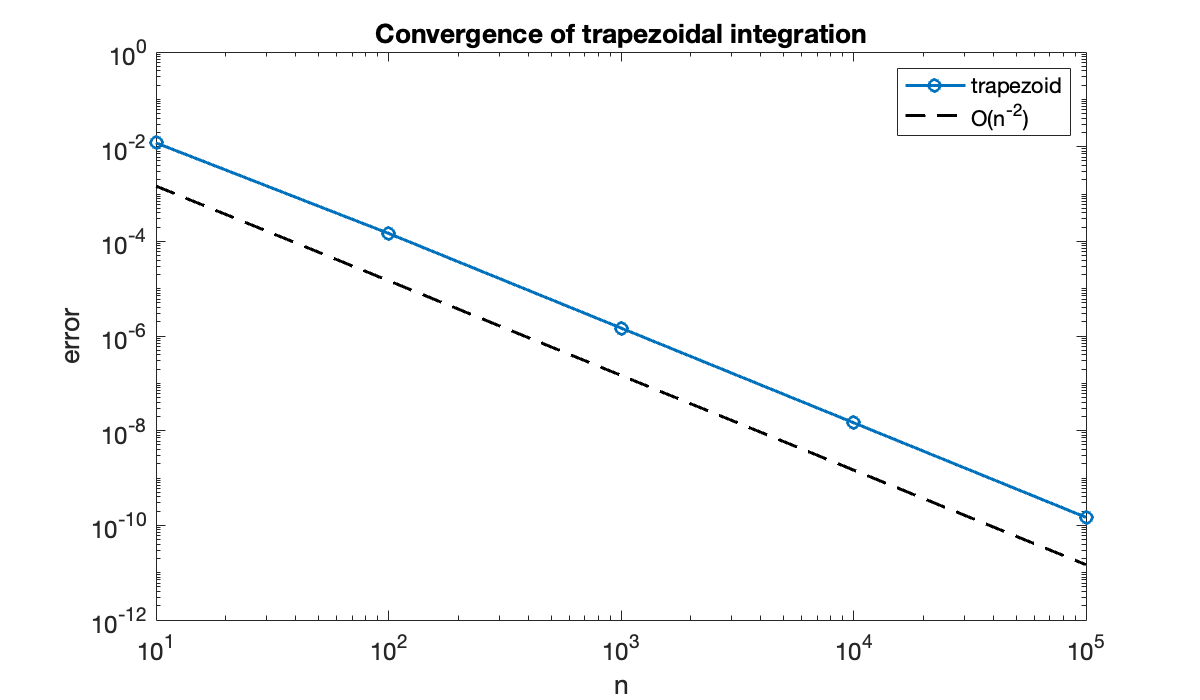
Example 5.6.3
We estimate using extrapolation. First we use quadgk to get an accurate value.
f = @(x) x.^2 .* exp(-2 * x);
a = 0; b = 2;
format long
I = integral(f, a, b, abstol=1e-14, reltol=1e-14)We start with the trapezoid formula on nodes.
N = 20; % the coarsest formula
n = N; h = (b - a) / n;
t = h * (0:n)';
y = f(t);We can now apply weights to get the estimate .
T = h * ( sum(y(2:n)) + y(1) / 2 + y(n+1) / 2 )Now we double to , but we only need to evaluate at every other interior node and apply (5.6.18).
n = 2*n; h = h / 2;
t = h * (0:n)';
T(2) = T(1) / 2 + h * sum( f(t(2:2:n)) )We can repeat the same code to double again.
n = 2*n; h = h / 2;
t = h * (0:n)';
T(3) = T(2) / 2 + h * sum( f(t(2:2:n)) )Let us now do the first level of extrapolation to get results from Simpson’s formula. We combine the elements T[i] and T[i+1] the same way for and .
S = (4 * T(2:3) - T(1:2)) / 3With the two Simpson values and in hand, we can do one more level of extrapolation to get a sixth-order accurate result.
R = (16*S(2) - S(1)) / 15We can make a triangular table of the errors:
err2 = T(:) - I;
err4 = [NaN; S(:) - I];
err6 = [NaN; NaN; R - I];
format short e
table(err2, err4, err6, variablenames=["order 2", "order 4", "order 6"])If we consider the computational time to be dominated by evaluations of , then we have obtained a result with about twice as many accurate digits as the best trapezoid result, at virtually no extra cost.
5.7 Adaptive integration¶
Example 5.7.1
This function gets increasingly oscillatory as increases.
f = @(x) (x + 1).^2 .* cos((2 * x + 1) ./ (x - 4.3));
clf
fplot(f, [0, 4], 2000)
xlabel('x'), ylabel(('f(x)'));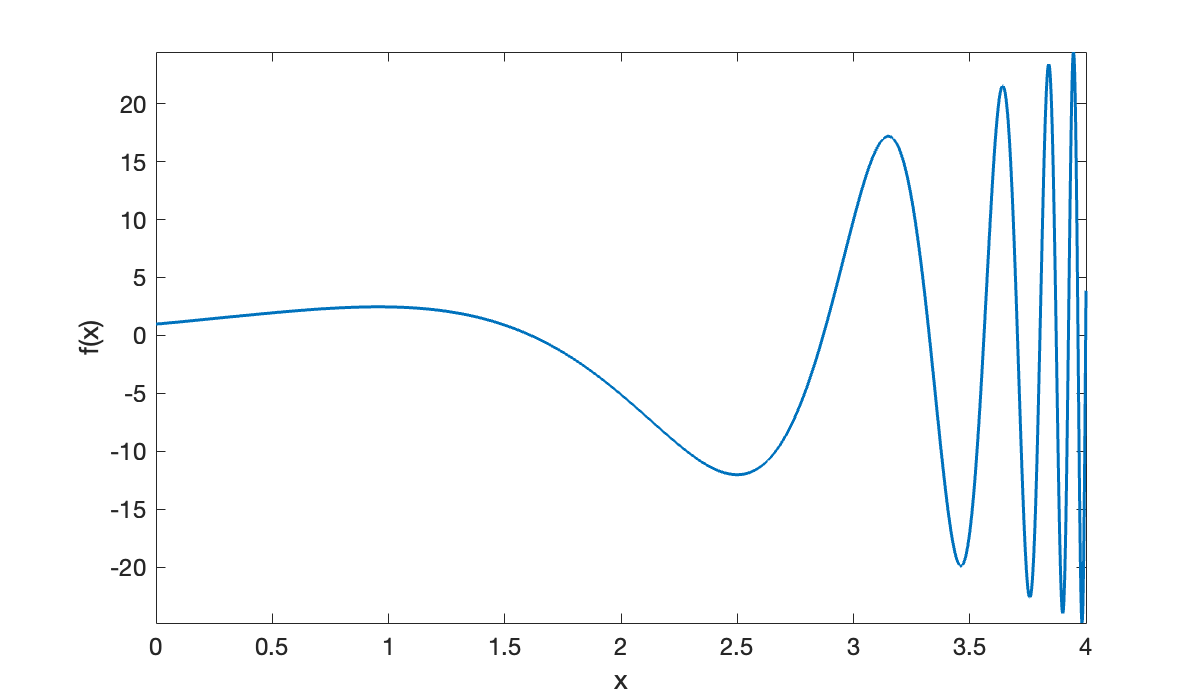
Accordingly, the trapezoid rule is more accurate on the left half of this interval than on the right half.
left_val = integral(f, 0, 2, abstol=1e-14, reltol=1e-14);
right_val = integral(f, 2, 4, abstol=1e-14, reltol=1e-14);
n = round(50 * 2 .^ (0:3)');
err = zeros(length(n), 2);
for i = 1:length(n)
T = trapezoid(f, 0, 2, n(i));
err(i, 1) = T - left_val;
T = trapezoid(f, 2, 4, n(i));
err(i, 2) = T - right_val;
end
table(n, err(:, 1), err(:, 2), variableNames=["n", "left error", "right error"])Both the picture and the numerical results suggest that more nodes should be used on the right half of the interval than on the left half.
Example 5.7.2
We’ll integrate the function from Demo 5.7.1.
f = @(x) (x + 1).^2 .* cos((2 * x + 1) ./ (x - 4.3));We perform the integration and show the nodes selected underneath the curve.
[Q, t] = intadapt(f, 0, 4, 0.001);
clf, fplot(f, [0, 4], 2000)
hold on
stem(t, f(t), '.-')
title('Adaptive node selection')
xlabel('x'), ylabel('f(x)')
fprintf("number of nodes = %d", length(t))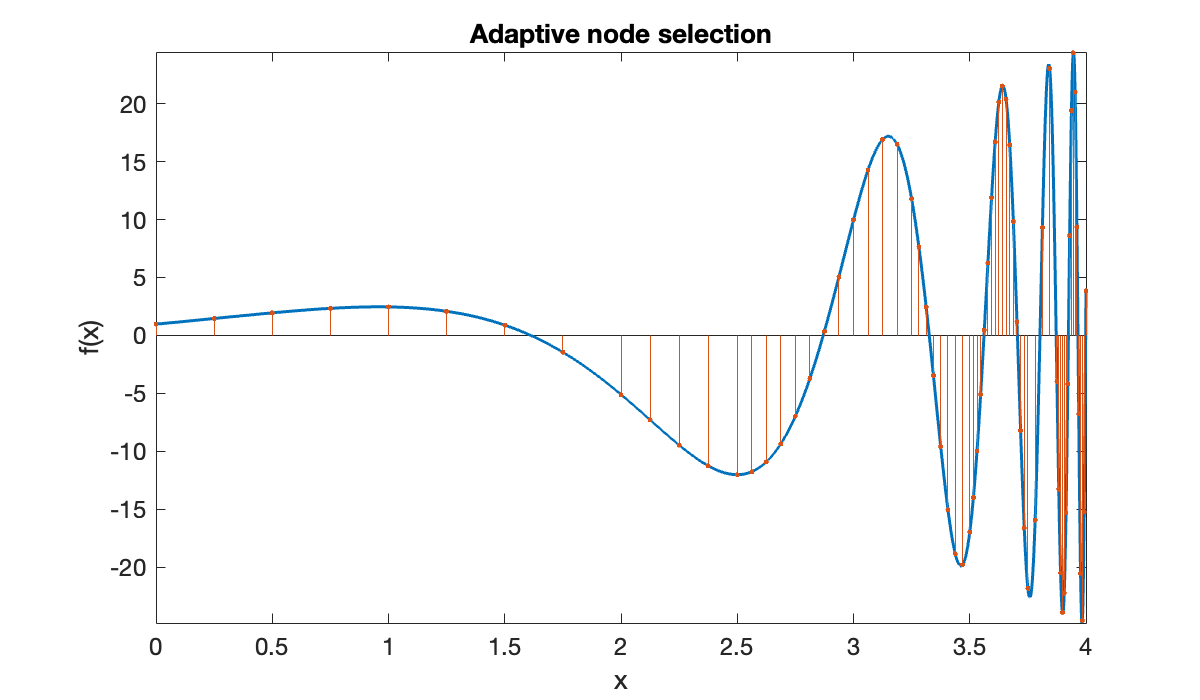
number of nodes = 69The error turns out to be a bit more than we requested. It’s only an estimate, not a guarantee.
I = integral(f, 0, 4, abstol=1e-14, reltol=1e-14); % 'exact' value
fprintf("error = %.2e", abs(Q - I))error = 2.20e-02Let’s see how the number of integrand evaluations and the error vary with the requested tolerance.
tol = 1 ./ 10.^(4:14)';
err = zeros(size(tol));
n = zeros(size(tol));
for k = 1:length(tol)
[A, t] = intadapt(f, 0, 4, tol(k));
err(k) = I - A;
n(k) = length(t);
end
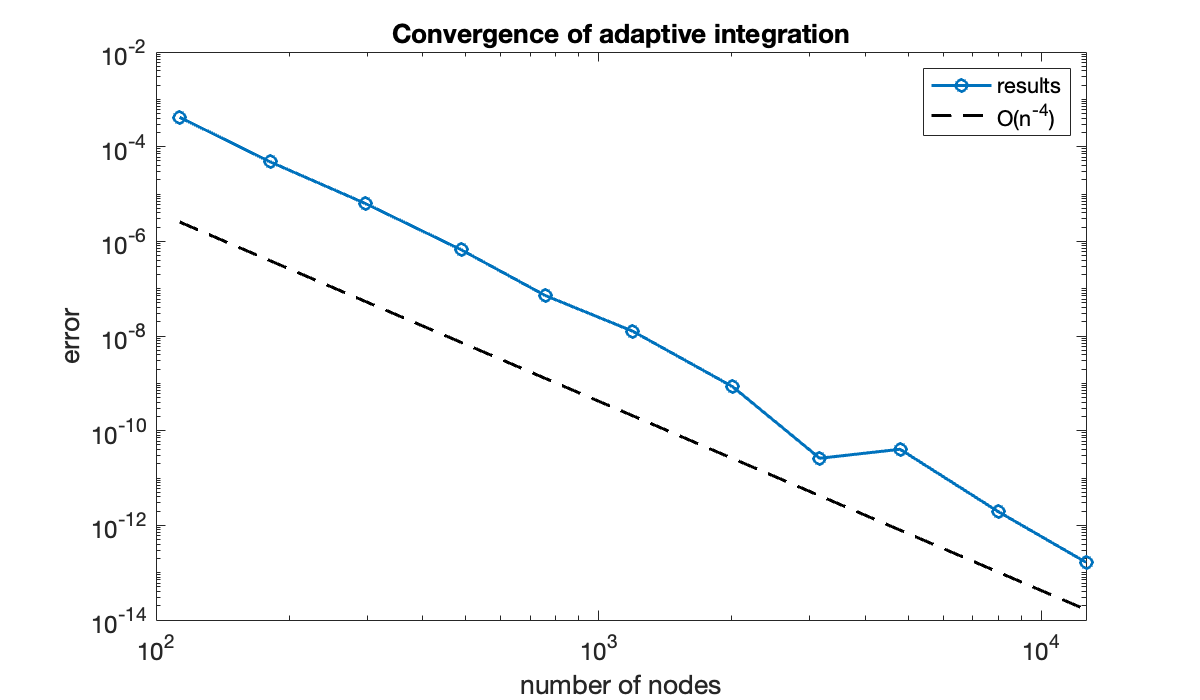
table(tol, err, n, variableNames=["tolerance", "error", "number of nodes"])As you can see, even though the errors are not smaller than the estimates, the two columns decrease in tandem. If we consider now the convergence not in , which is poorly defined now, but in the number of nodes actually chosen, we come close to the fourth-order accuracy of the underlying Simpson scheme.
clf
loglog(n, abs(err), "-o", displayname="results")
xlabel("number of nodes"), ylabel("error")
title("Convergence of adaptive integration")
order4 = 0.1 * abs(err(end)) * (n / n(end)).^(-4);
hold on
loglog(n, order4, "k--", displayname="O(n^{-4})")
legend();