Skip to article frontmatterSkip to article content

Chapter 6

Functions

Euler’s method for an initial-value problem
eulerivp.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function [t, u] = eulerivp(ivp, a, b, n)
% EULERIVP   Euler's method for a scalar initial-value problem.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   n       number of time steps (integer)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Define time discretization.
h = (b - a) / n;
t = a + (0:n) * h;

% Initialize solution array.
u = zeros(length(u0), n+1);
u(:, 1) = u0;

% Time stepping.
for i = 1:n
  u(:, i+1) = u(:, i) + h * du_dt(t(i), u(:, i), p);
end
About the code

The ivp input argument is the same structure that is used with the built-in solve solvers. The outputs t and u are row vectors of the same length, like the fields in a solution object output by solve. While the entries of u could be simplified to u(1), u(i), etc., we chose a column-access syntax like u(:, i) that will prove useful for what’s coming next in the chapter.

Improved Euler method for an IVP
ie2.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function [t, u] = ie2(ivp, a, b, n)
% IE2    Improved Euler method for an IVP.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   n       number of time steps (integer)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Define time discretization.
h = (b - a) / n;   
t = a + h * (0:n)';

% Initialize solution array. 
u = zeros(length(u0), n+1);
u(:, 1) = u0(:);

% Time stepping. 
for i = 1:n 
    uhalf = u(:, i) + h/2 * du_dt(t(i), u(:, i), p);
    u(:, i+1) = u(:, i) + h * du_dt(t(i) + h/2, uhalf, p);
end
Fourth-order Runge-Kutta for an IVP
rk4.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function [t, u] = rk4(ivp, a, b, n)
% RK4    Fourth-order Runge-Kutta for an IVP.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   n       number of time steps (integer)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Define time discretization.
h = (b - a) / n;   
t = a + h * (0:n)';

% Initialize solution array. 
u = zeros(length(u0), n+1);
u(:, 1) = u0(:);

% Time stepping.
for i = 1:n
  k1 = h * du_dt( t(i),       u(:, i)       , p);
  k2 = h * du_dt( t(i) + h/2, u(:, i) + k1/2, p );
  k3 = h * du_dt( t(i) + h/2, u(:, i) + k2/2, p );
  k4 = h * du_dt( t(i) + h,   u(:, i) + k3  , p);
  u(:, i+1) = u(:, i) + (k1 + 2*(k2 + k3) + k4) / 6;
end
Adaptive IVP solver based on embedded RK formulas
rk23.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function [t, u] = rk23(ivp, a, b, tol)
% RK23   Adaptive IVP solver based on embedded RK formulas.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   tol     global error target (positive scalar)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Initialize for the first time step.
t = a;
u(:, 1) = u0(:);  i = 1;
h = 0.5 * tol^(1/3);
s1 = du_dt(t(1), u(:, 1) ,p);

% Time stepping.
while t(i) < b
    % Detect underflow of the step size.
    if t(i) + h == t(i)
        warning('Stepsize too small near t=%.6g.',t(i))
        break  % quit time stepping loop
    end
    
    % New RK stages.
    s2 = du_dt(t(i) + h/2,   u(:, i) + (h/2)   * s1, p);
    s3 = du_dt(t(i) + 3*h/4, u(:, i) + (3*h/4) * s2, p);
    unew2 = u(:, i) + h * (2*s1 + 3*s2 + 4*s3) / 9;    % 2rd order solution
    s4 = du_dt(t(i) + h, unew2, p );
    err = h * (-5*s1/72 + s2/12 + s3/9 - s4/8);        % 2nd/3rd order difference
    E = norm(err, Inf);                                % error estimate
    maxerr = tol * (1 + norm(u(:, i), Inf));           % relative/absolute blend
    
    % Accept the proposed step? 
    if E < maxerr     % yes 
        t(i+1) = t(i) + h;
        u(:, i+1) = unew2;
        i = i+1;
        s1 = s4;      % use FSAL property
    end
    
    % Adjust step size. 
    q = 0.8 * (maxerr/E)^(1/3);       % conservative optimal step factor
    q = min(q, 4);                    % limit stepsize growth
    h = min(q*h, b - t(i));           % don't step past the end
end
About the code

The check t(i) + h == t(i)on line 24 is to detect when hh has become so small that it no longer changes the floating-point value of tit_i. This may be a sign that the underlying exact solution has a singularity near t=tit=t_i, but in any case, the solver must halt by using a break statement to exit the loop.

On line 36, we use a combination of absolute and relative tolerances to judge the acceptability of a solution value, as in (5.7.6). In lines 47--49 we underestimate the step factor qq a bit and prevent a huge increase in the step size, since a rejected step is expensive, and then we make sure that our final step doesn’t take us past the end of the domain.

Finally, line 43 exploits a subtle property of the BS23 formula called first same as last (FSAL). While (6.5.5) calls for four stages to find the paired second- and third-order estimates, the final stage computed in stepping from tit_i to ti+1t_{i+1} is identical to the first stage needed to step from ti+1t_{i+1} to ti+2t_{i+2}. By repurposing s4 as s1 for the next pass, one of the stage evaluations comes for free, and only three evaluations of ff are needed per successful step.

4th-order Adams–Bashforth formula for an IVP
ab4.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function [t, u] = ab4(ivp, a, b, n)
%AB4     4th-order Adams-Bashforth formula for an IVP.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   n       number of time steps (integer)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Define time discretization.
h = (b - a) / n;   
t = a + h * (0:n)';

% Constants in the AB4 method.
k = 4;  
sigma = [55; -59; 37; -9] / 24;  

% Find starting values by RK4.
[ts, us] = rk4(ivp, a, a + (k-1)*h, k-1);
u = zeros(length(u0), n+1);
u(:, 1:k) = us(:, 1:k);

% Compute history of u' values, from oldest to newest.
f = zeros(length(u0), k);
for i = 1:k-1
  f(:, k-i) = du_dt(t(i), u(:, i), p);
end

% Time stepping.
for i = k:n
  f = [du_dt(t(i), u(:, i), p), f(:, 1:k-1)];   % new value of du/dt
  u(:, i+1) = u(:, i) + h * (f * sigma);        % advance one step
end
About the code

Line 21 sets sigma to be the coefficients of the generating polynomial σ(z)\sigma(z) of AB4. Lines 24--26 set up the IVP over the time interval a≤t≤a+3ha \le t \le a+3 h, call rk4 to solve it using the step size hh, and use the result to fill the first four values of the solution. Then lines 29--32 compute the vector [f2,f1,f0][f_2,f_1,f_0].

Line 36 computes fif_i, based on the most recent solution value and time. That goes into the first column of f, followed by the three values that were previously most recent. These are the four values that appear in (6.7.1). Each particular fif_i value starts at the front of f, moves through each position in the vector over three iterations, and then is forgotten.

2nd-order Adams–Moulton (trapezoid) formula for an IVP
am2.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function [t, u] = am2(ivp, a, b, n)
% AM2    2nd-order Adams-Moulton (trapezoid) formula for an IVP.
% Input:
%   ivp     structure defining the IVP
%   a, b    endpoints of time interval (scalars)
%   n       number of time steps (integer)
% Output:
%   t       selected nodes (vector, length n+1)
%   u       solution values (array, m by (n+1))

du_dt = ivp.ODEFcn;
u0 = ivp.InitialValue;
p = ivp.Parameters;

% Define time discretization.
h = (b - a) / n;   
t = a + h * (0:n)';

u = zeros(length(u0), n+1);
u(:, 1) = u0(:);

% Time stepping.
for i = 1:n
  % Data that does not depend on the new value.
  known = u(:,i) + h/2 * du_dt(t(i), u(:, i), p);
  % Find a root for the new value. 
  unew = levenberg(@trapzero, known);
  u(:, i+1) = unew(:, end);
end

% This function defines the rootfinding problem at each step.
function F = trapzero(z)
    F = z - h/2 * du_dt(t(i+1), z, p) - known;
end

end  % main function
About the code

Lines 32--34 define the function g\mathbf{g}. This is sent to levenberg in line~27 to find the new solution value, using an Euler half-step as its starting value. A robust code would have to intercept the case where levenberg fails to converge, but we have ignored this issue for the sake of brevity.

Examples

6.1 Basics of IVPs

Example 6.1.2

Let’s use it to define and solve an initial-value problem for u′=sin⁡[(u+t)2]u'=\sin[(u+t)^2] over t∈[0,4]t \in [0,4], such that u(0)=−1u(0)=-1. To create an initial-value problem for u(t)u(t), you must create an ode with a function that computes u′u' and an initial condition for uu. Then you create a solution by calling solve with a time interval.

Tip

Most real ODE problems contain parameters that are constant during the solution but that can change from one problem instance to the next. Accordingly, we define the ODE function below to accept a third argument, p, which is a vector of parameters. We always include this argument for consistency, even when there are no parameters.

ivp = ode;
ivp.ODEFcn = @(t, u, p) sin((t + u)^2);
ivp.InitialTime = 0;
ivp.InitialValue = -1;
sol = solve(ivp, 0, 4);

The resulting solution object has fields Time and Solution that contain the approximate values of the solution at automatically chosen times in the interval you provided.

clf
plot(sol.Time, sol.Solution, '-o')
xlabel("t")
ylabel("u(t)")
title(("Solution of an IVP"));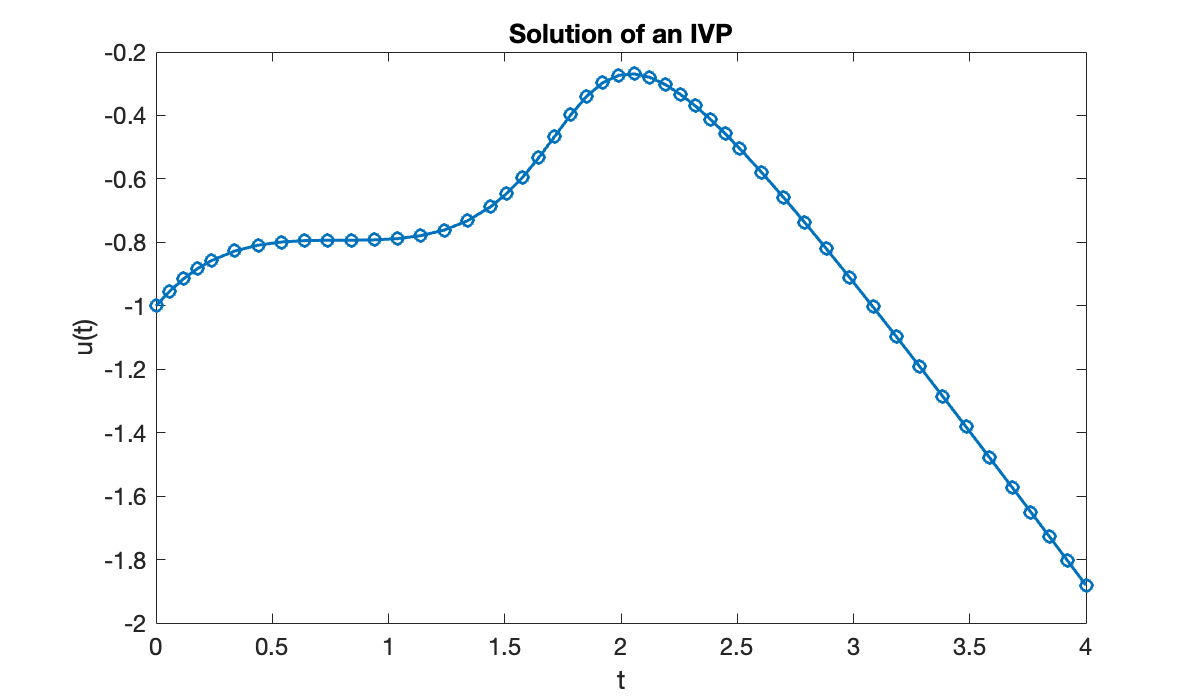
Image produced in Jupyter

You might want to know the solution at particular times other than the ones selected by the solver. That requires an interpolation, which is done by solutionFcn.

u = solutionFcn(ivp, 0, 10);
u(0:5)
Loading...
Example 6.1.3

The equation u′=(u+t)2u'=(u+t)^2 gives us some trouble.

ivp = ode;
ivp.ODEFcn = @(t, u, p) (t + u)^2;
ivp.InitialTime = 0;
ivp.InitialValue = 1;
sol = solve(ivp, 0, 1);
Warning: Failure at t=7.853789e-01.  Unable to meet integration tolerances without reducing the step size below the smallest value allowed (1.776357e-15) at time t.

The warning message we received can mean that there is a bug in the formulation of the problem. But if everything has been done correctly, it suggests that the solution may not exist past the indicated time. This is a possibility in nonlinear ODEs.

clf
semilogy(sol.Time, sol.Solution)
xlabel("t")
ylabel("u(t)")
title(("Finite-time blowup"));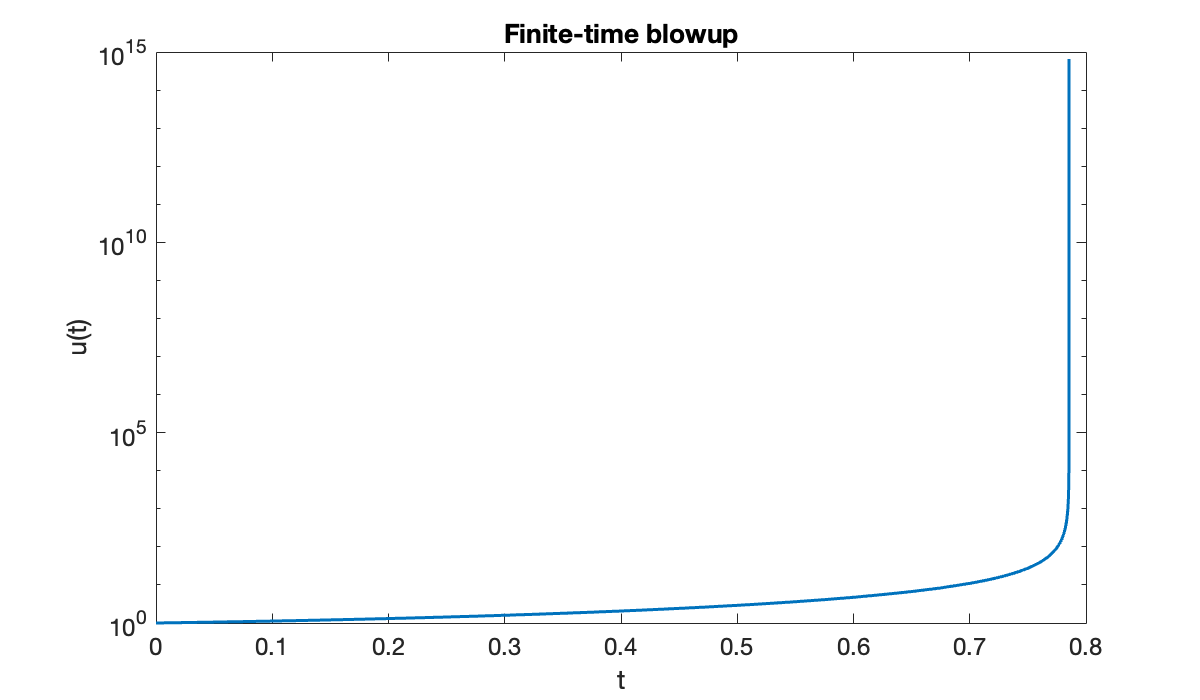
Image produced in Jupyter
Example 6.1.5

Consider the ODEs u′=uu'=u and u′=−uu'=-u. In each case we compute ∂f/∂u=±1\partial f/\partial u = \pm 1, so the condition number bound from Theorem 6.1.2 is eb−ae^{b-a} in both problems. However, they behave quite differently. In the case of exponential growth, u′=uu'=u, the bound is the actual condition number.

clf
for u0 = [0.7, 1, 1.3]    % initial values
    fplot(@(t) exp(t) * u0, [0, 3]), hold on
end
xlabel('t')
ylabel('u(t)')
title(('Exponential divergence of solutions'));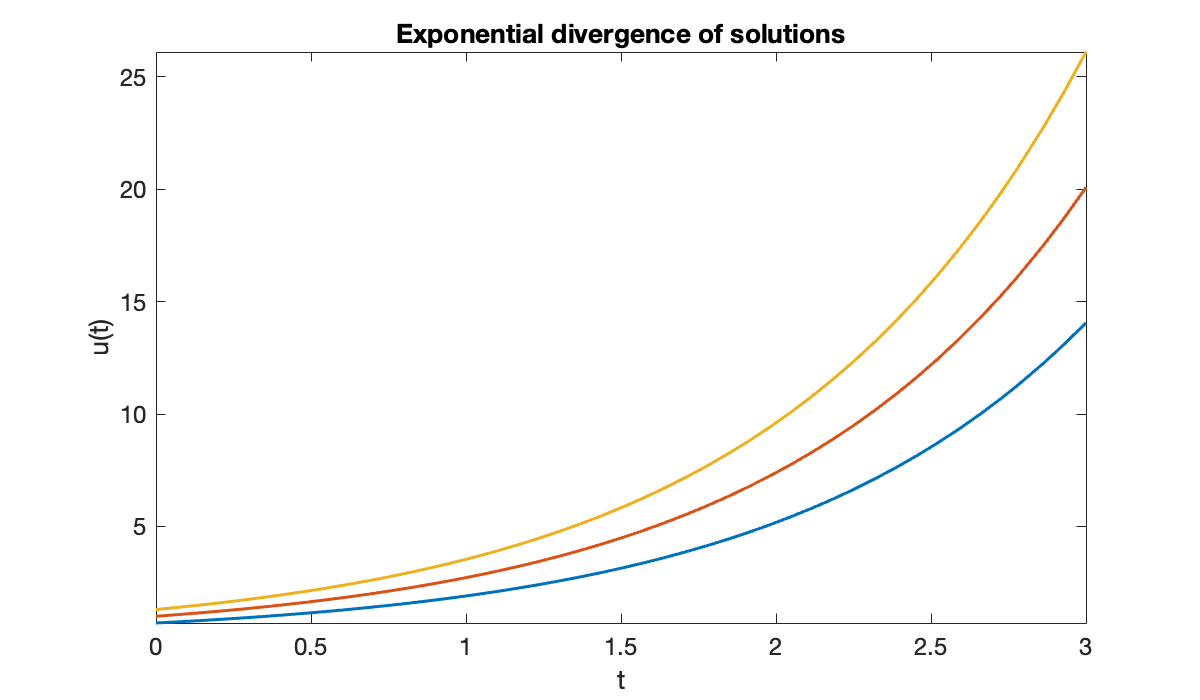
Image produced in Jupyter

But with u′=−uu'=-u, solutions actually get closer together with time.

clf
for u0 = [0.7, 1, 1.3]    % initial values
    fplot(@(t) exp(-t) * u0, [0, 3]), hold on
end
xlabel('t')
ylabel('u(t)')
title(('Exponential convergence of solutions'));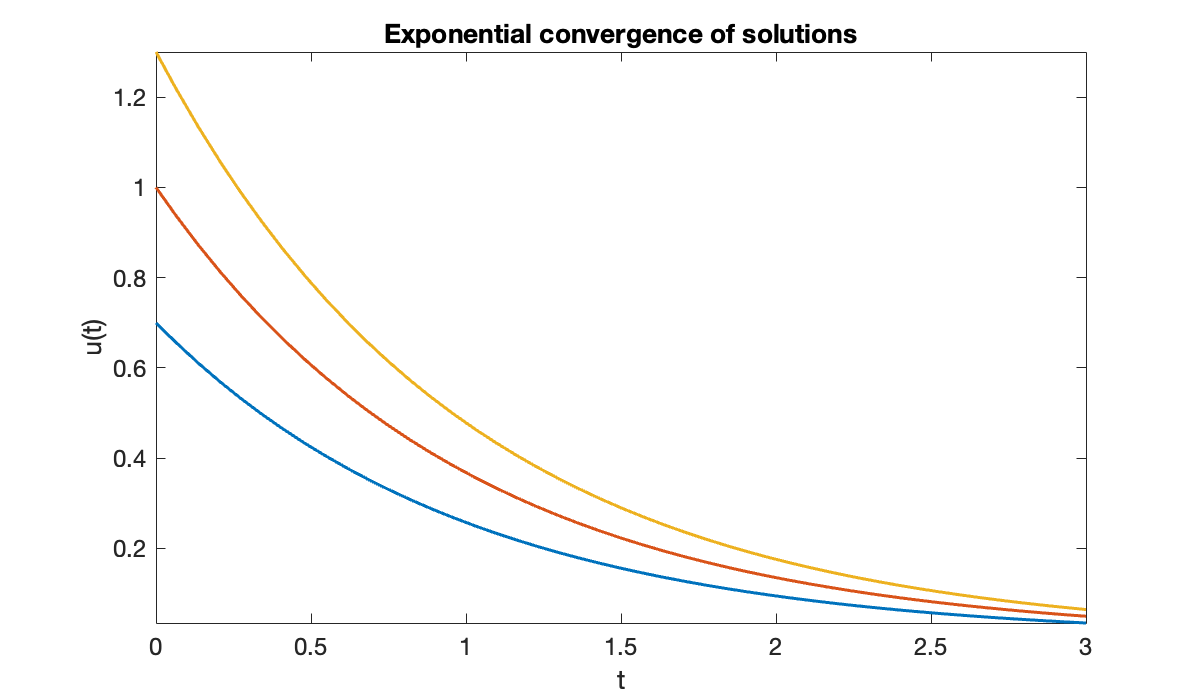
Image produced in Jupyter

In this case the actual condition number is one, because the initial difference between solutions is the largest over all time. Hence the exponentially growing bound eb−ae^{b-a} is a gross overestimate.

6.2 Euler’s method

Example 6.2.1

We consider the IVP u′=sin⁡[(u+t)2]u'=\sin[(u+t)^2] over 0≤t≤40\le t \le 4, with u(0)=−1u(0)=-1. We need to define the function for the right-hand side of the ODE, the interval for the independent variable, and the initial value.

ivp = ode;
ivp.ODEFcn = @(t, u, p) sin((t + u)^2);
ivp.InitialValue = -1;
a = 0;  b = 4;

Here is the call to Function 6.2.2.

[t, u] = eulerivp(ivp, a, b, 20);
clf, plot(t, u, '.-')
xlabel('t')
ylabel('u(t)')
title(('Solution by Euler''s method'));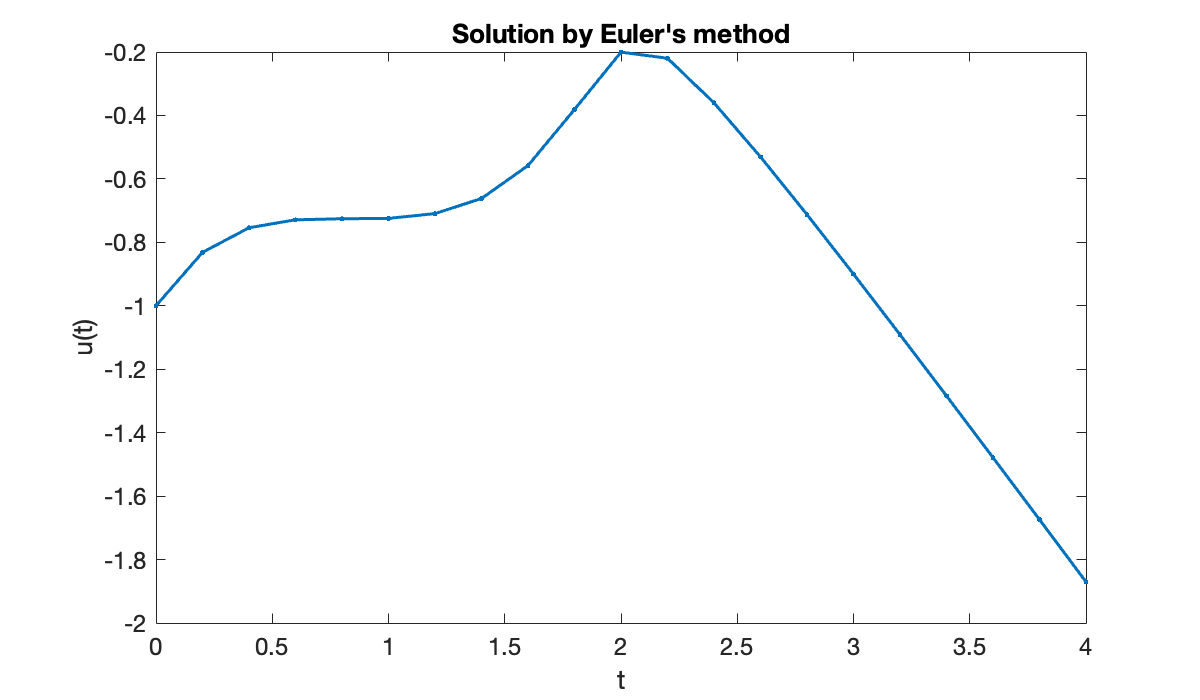
Image produced in Jupyter

We could define a different interpolant to get a smoother picture above, but the derivation of Euler’s method assumed a piecewise linear interpolant. We can instead request more steps to make the interpolant look smoother.

[t, u] = eulerivp(ivp, a, b, 50);
hold on, plot(t, u, '.-')
legend('20 steps', '50 steps');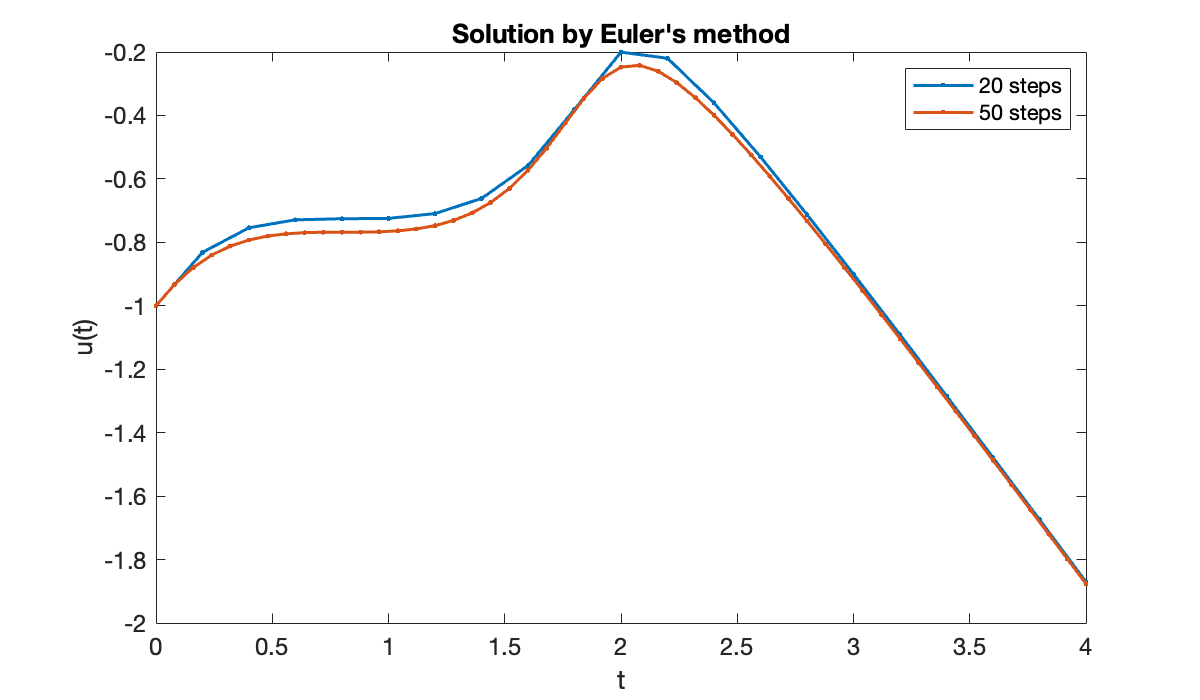
Image produced in Jupyter

Increasing nn changed the solution noticeably. Since we know that interpolants and finite differences become more accurate as h→0h\to 0, we should anticipate the same behavior from Euler’s method. We don’t have an exact solution to compare to, so we will use a built-in solver to construct an accurate reference solution.

ivp.AbsoluteTolerance = 1e-13;
ivp.RelativeTolerance = 1e-13;
u_exact = solutionFcn(ivp, a, b);

Now we can perform a convergence study.

n = round(5 * 10.^(0:0.5:3));
err = [];
for k = 1:length(n)
    [t, u] = eulerivp(ivp, a, b, n(k));
    err(k) = norm(u_exact(t) - u, Inf);
end
table(n', err', VariableNames=["n", "inf-norm error"])
Loading...

The error is approximately cut by a factor of 10 for each increase in nn by the same factor. A log-log plot also confirms first-order convergence. Keep in mind that since h=(b−a)/nh=(b-a)/n, it follows that O(h)=O(n−1)O(h)=O(n^{-1}).

clf
loglog(n, err, 'o-')
hold on, loglog(n, 0.5 * err(end) * (n / n(end)).^(-1), '--')
xlabel('n')
ylabel('inf-norm error')
title('Convergence of Euler''s method')
legend('error', 'O(n^{-1})', 'location', 'southwest');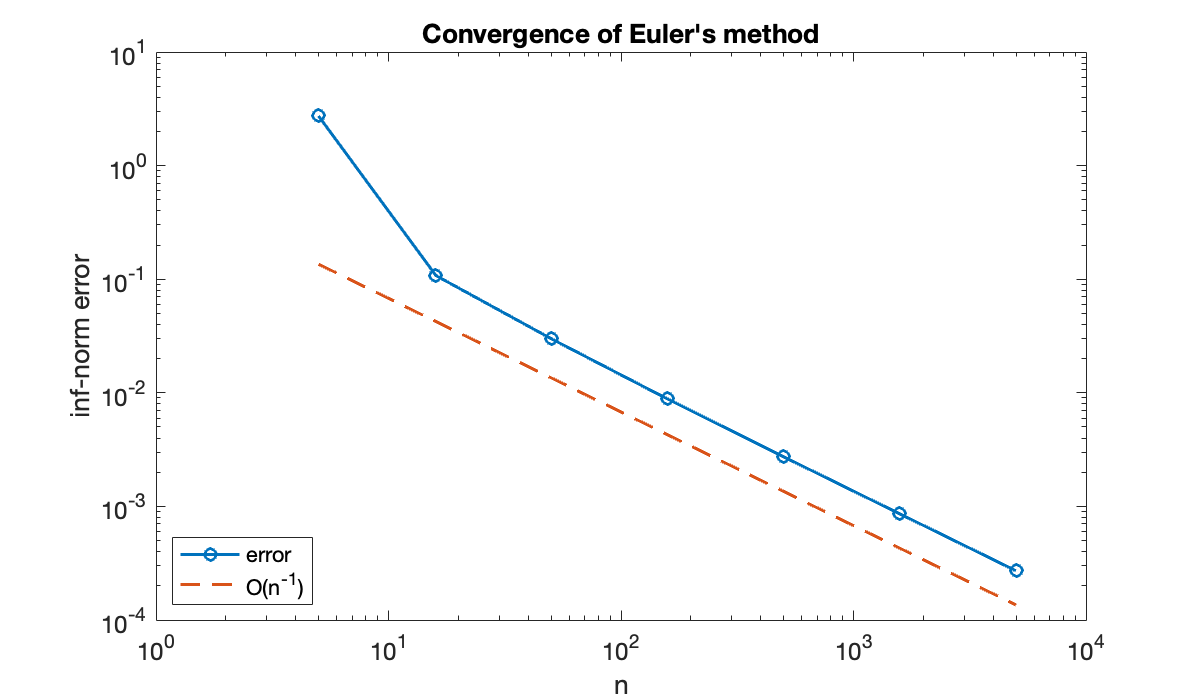
Image produced in Jupyter

6.3 IVP systems

Example 6.3.2

We encode the predator–prey equations via a function, defined here externally.

f63_predprey.m
function du_dt = predprey(t, u, p)
    alpha = p(1);  beta = p(2);
    y = u(1);      z = u(2);
    s = (y * z) / (1 + beta * y);  % appears in both equations
    du_dt = [ y * (1 - alpha * y) - s;  -z + s ];
end

The values of alpha and beta are parameters that influence the solution of the IVP. We use the Parameters field of the IVP object to define them for the solver, which in turn passes them as the third argument into our ODE function.

u0 = [1; 0.01];    % column vector
p = [0.1, 0.25];
ivp = ode;
ivp.ODEFcn = @f63_predprey;
ivp.InitialValue = u0;
ivp.Parameters = p;
sol = solve(ivp, 0, 60);
size(sol.Solution)
Loading...

Each column of the Solution field is the solution vector u\mathbf{u} at a particular time; each row is a component of u\mathbf{u} over all time.

clf
plot(sol.Time, sol.Solution)
xlabel("t")
ylabel("u(t)")
title('Predator-prey solution')
legend('prey', 'predator');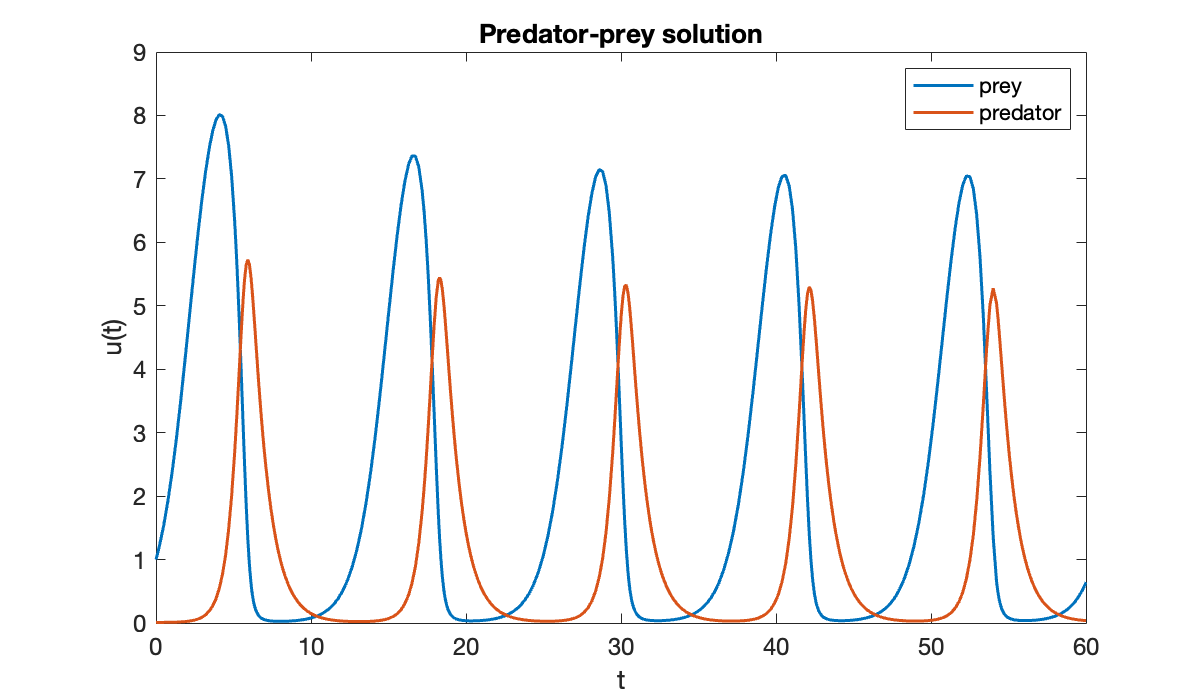
Image produced in Jupyter

We can also use Function 6.2.2 to find the solution.

[t, u] = eulerivp(ivp, 0, 60, 1200);
hold on
plot(t, u, '.')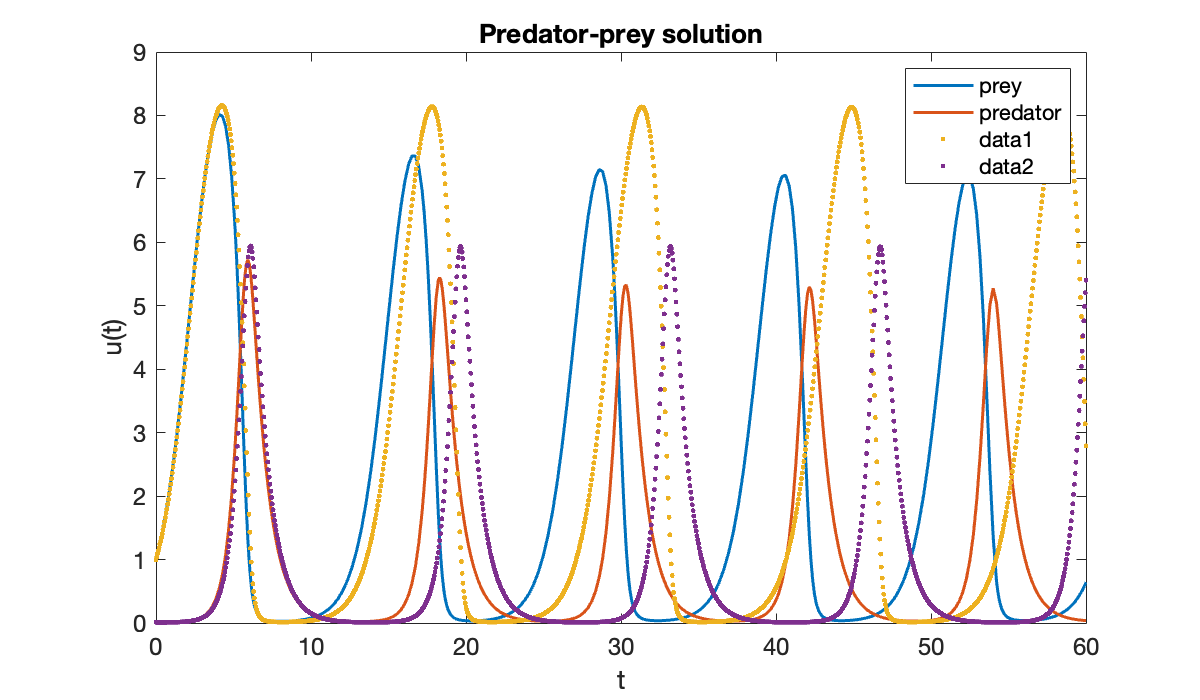
Image produced in Jupyter

Notice above that the accuracy of the Euler solution deteriorates rapidly.

When there are just two components, it’s common to plot the solution in the phase plane, i.e., with u1u_1 and u2u_2 along the axes and time as a parameterization of the curve.

clf
plot(u(1, :), u(2, :))
title("Predator-prey in the phase plane")
xlabel("y")
ylabel(("z"));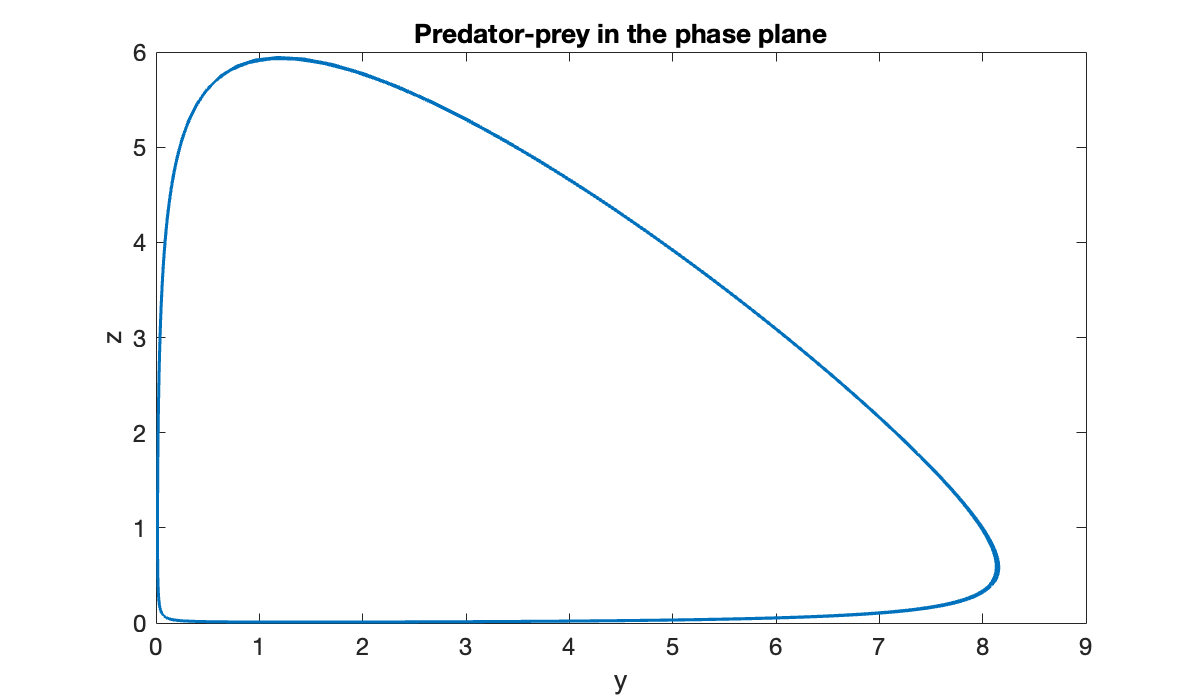
Image produced in Jupyter

From this plot we can deduce that the solution approaches a periodic one, which in the phase plane is represented by a closed loop.

Example 6.3.5

Let’s implement the coupled pendulums from Example 6.3.4. The pendulums will be pulled in opposite directions and then released together from rest.

f63_pendulums.m
function udot = pendulums(t, u, p)
    gamma = p(1);  L = p(2);  k = p(3);
    g = 9.8;
    udot = zeros(4, 1);
    udot(1:2) = u(3:4);
    udot(3) = -gamma * u(3) - (g / L) * sin(u(1)) + k * (u(2) - u(1));
    udot(4) = -gamma * u(4) - (g / L) * sin(u(2)) + k * (u(1) - u(2));
end

u0 = [1.25; -0.5; 0; 0];
a = 0; b = 50;

First we check the behavior of the system when the pendulums are uncoupled, i.e., when k=0k=0.

Tip

Here OutputVariables is used to restrict output to just u1u_1 and u2u_2.

params =[0.01, 0.5, 0];    % gamma, L, k
ivp = ode(ODEFcn=@f63_pendulums, InitialValue=u0, Parameters=params);
theta = solutionFcn(ivp, a, b, OutputVariables = 1:2);
t = linspace(a, b, 1001);
clf, plot(t, theta(t))
xlabel("t");  ylabel("angle")
title("Uncoupled pendulums")
legend("\theta_1", "\theta_2");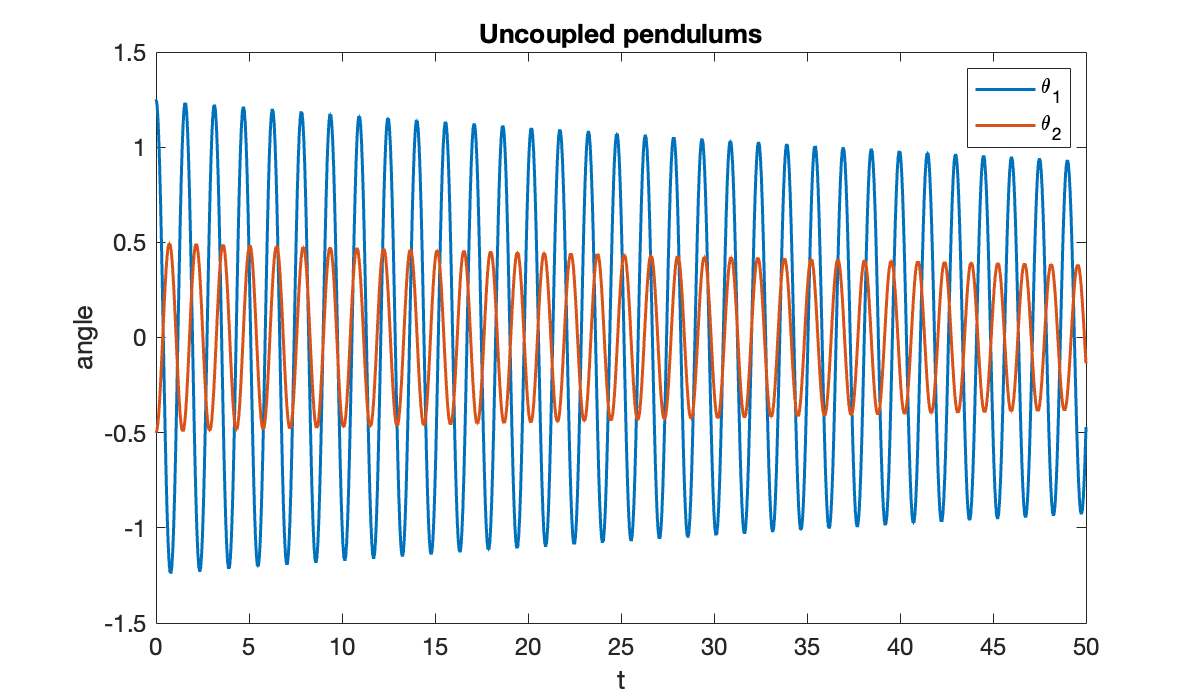
Image produced in Jupyter

You can see that the pendulums swing independently. Because the model is nonlinear and the initial angles are not small, they have slightly different periods of oscillation, and they go in and out of phase.

With coupling activated, a different behavior is seen.

params(3) = 1;
ivp = ode(ODEFcn=@f63_pendulums, InitialValue=u0, Parameters=params);
theta = solutionFcn(ivp, a, b, OutputVariables = 1:2);
clf, plot(t, theta(t))
xlabel("t");  ylabel("angle")
title("Coupled pendulums")
legend("\theta_1", "\theta_2");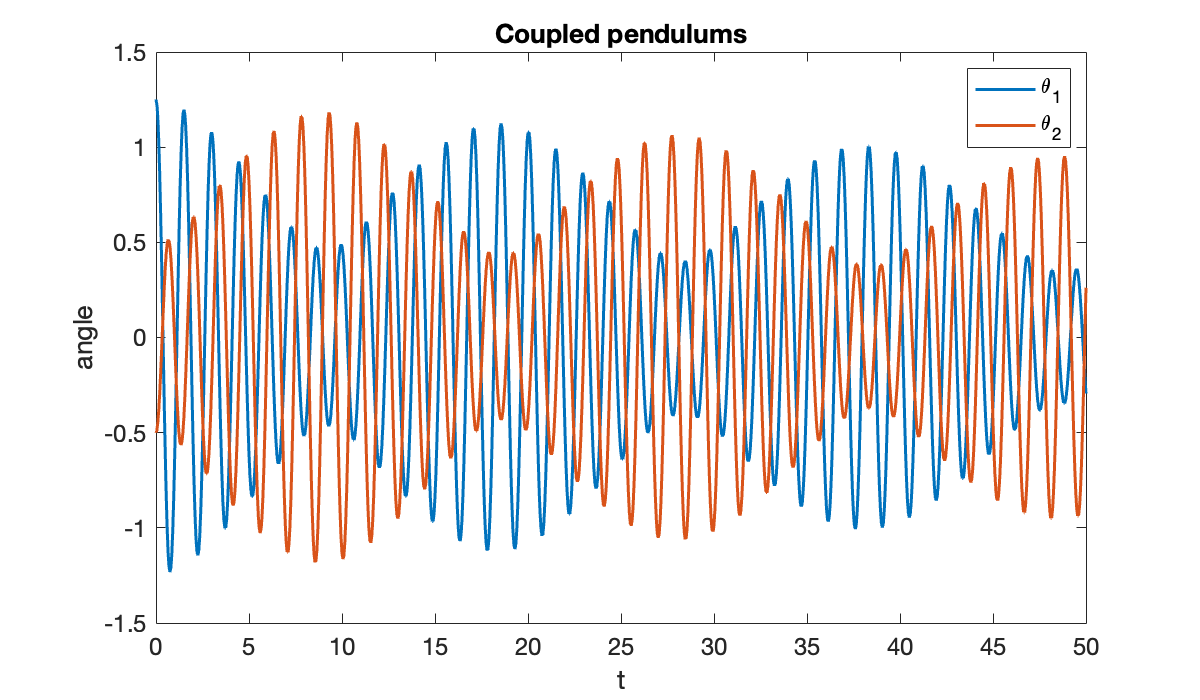
Image produced in Jupyter

The coupling makes the pendulums swap energy back and forth.

6.4 Runge–Kutta methods

Example 6.4.1

We solve the IVP u′=sin⁡[(u+t)2]u'=\sin[(u+t)^2] over 0≤t≤40\le t \le 4, with u(0)=−1u(0)=-1.

ivp = ode;
ivp.ODEFcn = @(t, u, p) sin((t + u)^2);
ivp.InitialValue = -1;
a = 0;  b = 4;

We use a built-in solver to construct an accurate approximation to the exact solution.

ivp.AbsoluteTolerance = 1e-13;
ivp.RelativeTolerance = 1e-13;
u_ref = solutionFcn(ivp, a, b);

Now we perform a convergence study of our two Runge–Kutta implementations.

n = round(2 * 10.^(0:0.5:3)');
err = zeros(length(n), 2);
for i = 1:length(n)
    [t, u] = ie2(ivp, a, b, n(i));
    err(i, 1) = norm(u_ref(t) - u, Inf);
    [t, u] = rk4(ivp, a, b, n(i));
    err(i, 2) = norm(u_ref(t) - u, Inf);
end

disp(table(n, err(:, 1), err(:, 2), variableNames=["n", "IE2 error", "RK4 error"]))
     n      IE2 error     RK4 error 

    ____    __________    __________


       2         1.769       0.82065

       6       0.51268       0.79192

      20      0.024059    0.00081269

      63     0.0022533    8.0622e-06

     200    0.00022242    7.6066e-08

     632    2.2253e-05     7.515e-10

    2000    2.2218e-06    7.6541e-12

The amount of computational work at each time step is assumed to be proportional to the number of stages. Let’s compare on an apples-to-apples basis by using the number of ff-evaluations on the horizontal axis.

clf, loglog([2*n 4*n], err, '-o')
hold on
loglog(2*n, 1e-5 * (n / n(end)) .^ (-2), '--')
loglog(4*n, 1e-10 * (n / n(end)) .^ (-4), '--')
xlabel("f-evaluations");  ylabel("inf-norm error")
title("Convergence of RK methods")
legend("IE2", "RK4", "O(n^{-2})", "O(n^{-4})", "location", "southwest");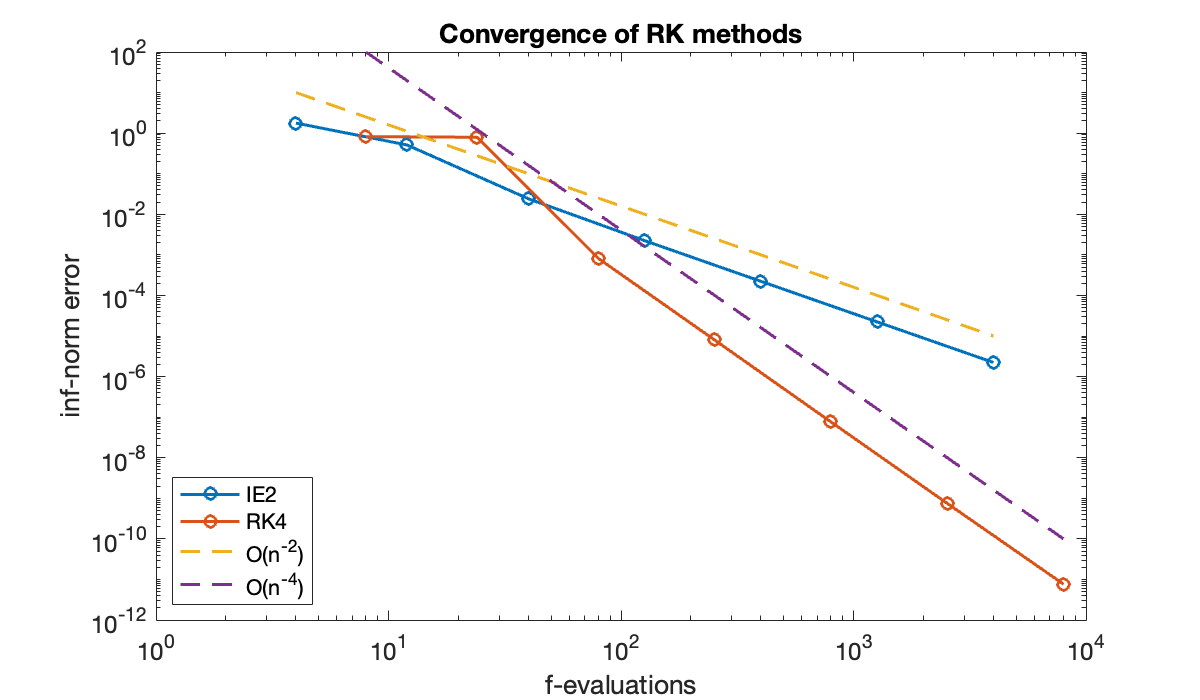
Image produced in Jupyter

The fourth-order variant is more efficient in this problem over a wide range of accuracy.

6.5 Adaptive Runge–Kutta

Example 6.5.1

Let’s run adaptive RK on u′=et−usin⁡uu'=e^{t-u\sin u}.

ivp = ode;
ivp.ODEFcn = @(t, u, p) exp(t - u * sin(u));
ivp.InitialValue = 0;
a = 0;  b = 5;

[t, u] = rk23(ivp, a, b, 1e-5);
clf, plot(t, u)
xlabel("t");  ylabel("u(t)")
title(("Adaptive IVP solution"));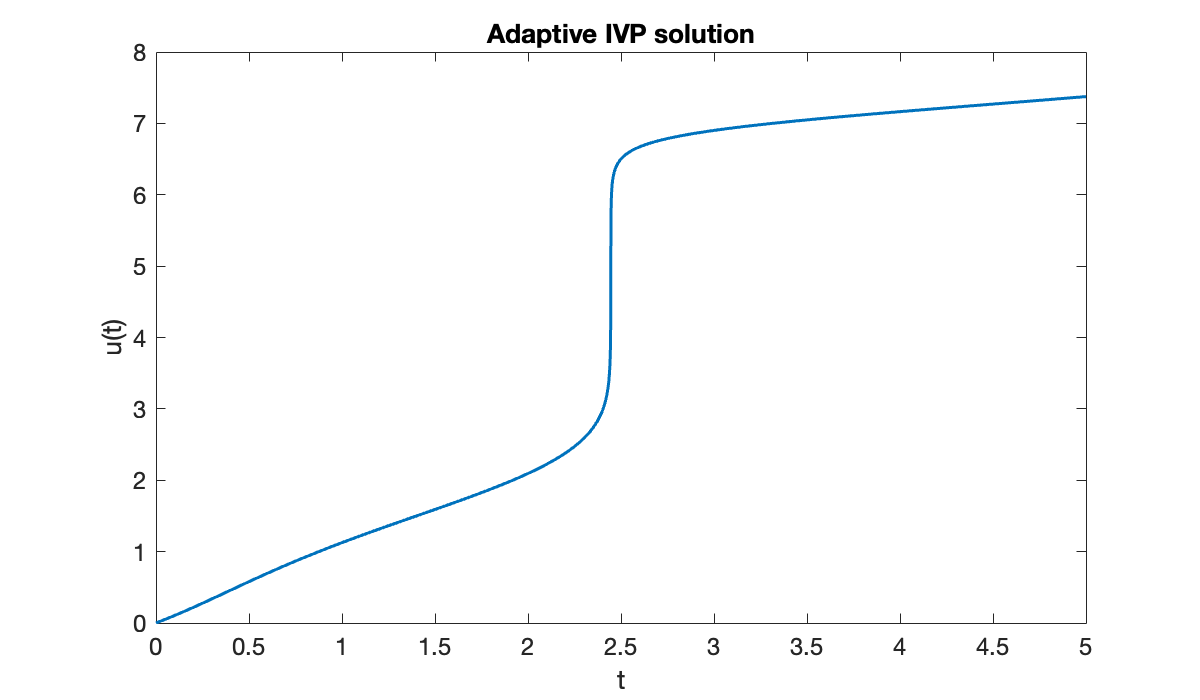
Image produced in Jupyter

The solution makes a very abrupt change near t=2.4t=2.4. The resulting time steps vary over three orders of magnitude.

Delta_t = diff(t);
semilogy(t(1:end-1), Delta_t) 
xlabel("t");  ylabel("step size")
title(("Adaptive step sizes"));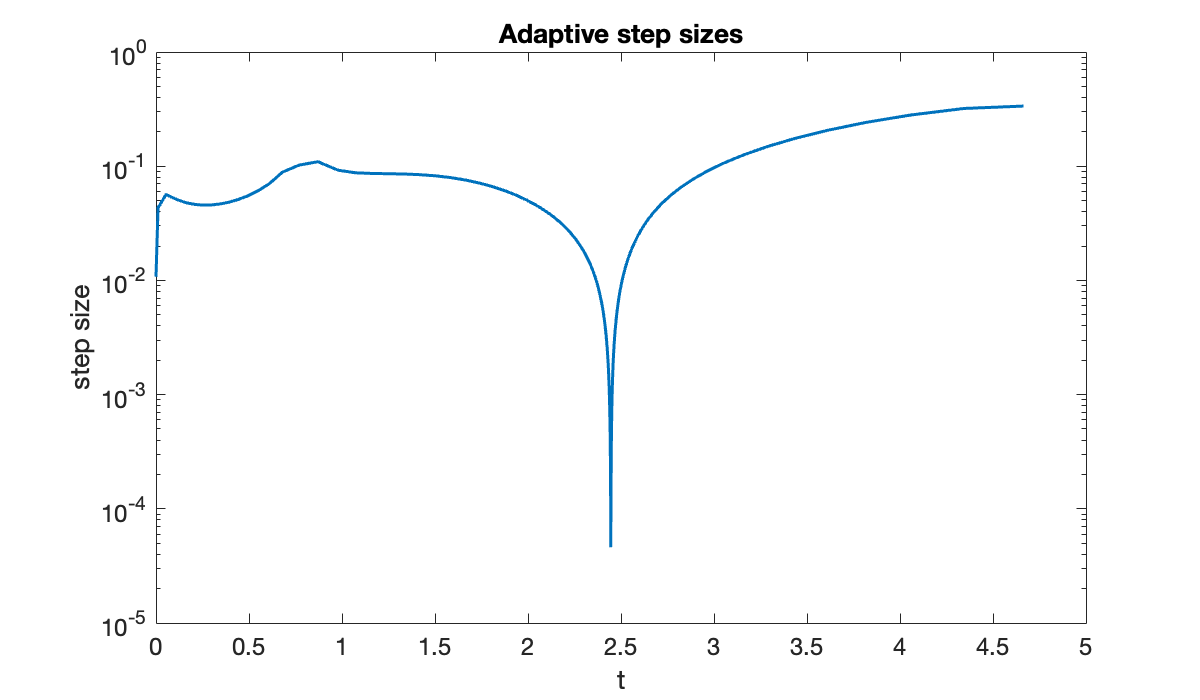
Image produced in Jupyter

If we had to run with a uniform step size to get this accuracy, it would be

fprintf("minimum step size = %.2e", min(Delta_t))
minimum step size = 
4.61e-05

On the other hand, the average step size that was actually taken was

fprintf("average step size = %.2e", mean(Delta_t))
average step size = 
3.21e-02

We took fewer steps by a factor of almost 1000! Even accounting for the extra stage per step and the occasional rejected step, the savings are clear.

Example 6.5.2

In Demo 6.1.3 we saw an IVP that appears to blow up in a finite amount of time. Because the solution increases so rapidly as it approaches the blowup, adaptive stepping is required even to get close.

ivp = ode;
ivp.ODEFcn = @(t, u, p) (t + u)^2;
ivp.InitialValue = 1;
[t, u] = rk23(ivp, 0, 1, 1e-5);
Warning: Stepsize too small near t=0.785409.

In fact, the failure of the adaptivity gives a decent idea of when the singularity occurs.

clf, semilogy(t, u)
xlabel("t");  ylabel("u(t)")
title("Adaptive solution near a singularity")

tf = t(end);
xline(tf, "linestyle", "--")
text(tf, 1e5, sprintf(" t = %.6f ", tf))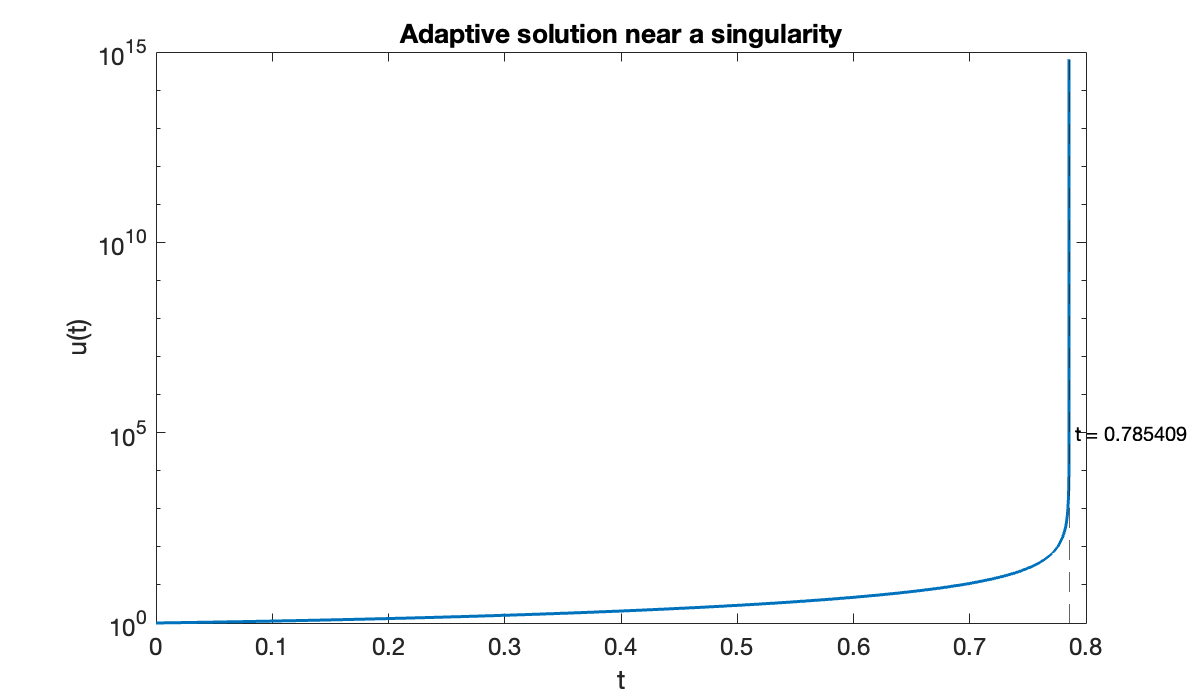
Image produced in Jupyter

6.6 Multistep methods

Example 6.7.1

We study the convergence of AB4 using the IVP u′=sin⁡[(u+t)2]u'=\sin[(u+t)^2] over 0≤t≤40\le t \le 4, with u(0)=−1u(0)=-1. As usual, a built-in solver is called to give an accurate reference solution.

ivp = ode;
ivp.ODEFcn = @(t, u, p) sin((t + u)^2);
ivp.InitialValue = -1;
a = 0;  b = 4;
ivp.AbsoluteTolerance = 1e-13;
ivp.RelativeTolerance = 1e-13;
u_ref = solutionFcn(ivp, a, b);

Now we perform a convergence study of the AB4 code.

n = round(4 * 10.^(0:0.5:3)');
err = zeros(size(n));
for i = 1:length(n)
    [t, u] = ab4(ivp, a, b, n(i));
    err(i) = norm(u_ref(t) - u, Inf);
end
disp(table(n, err, variableNames=["n", "inf-norm error"]))
     n      inf-norm error

    ____    ______________


       4         0.50044  

      13          1.3913  

      40       0.0062781  

     126      9.9494e-05  

     400       1.096e-06  

    1265      1.1276e-08  

    4000      1.1331e-10

The method should converge as O(h4)O(h^4), so a log-log scale is appropriate for the errors.

clf, loglog(n, err, '-o')
hold on
loglog(n, 0.5 * err(end) * (n / n(end)) .^ (-4), '--')
xlabel("n");  ylabel("inf-norm error")
title("Convergence of AB4")
legend("AB4", "O(n^{-4})", location="southwest");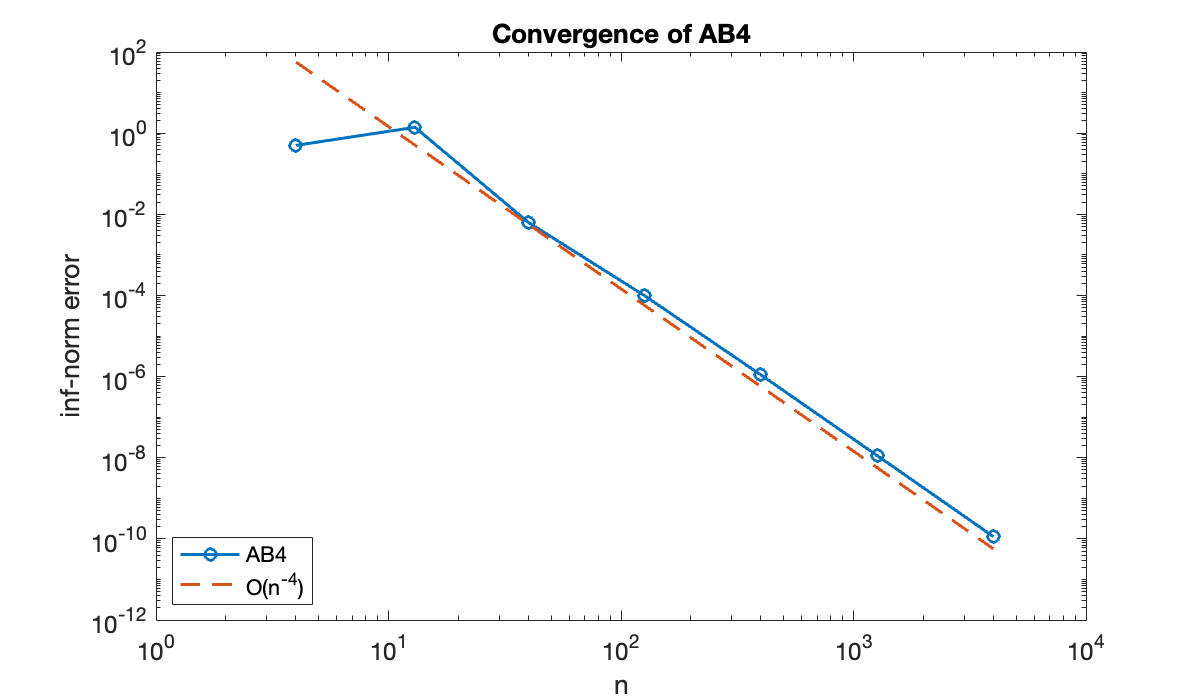
Image produced in Jupyter
Example 6.7.2

The following simple ODE uncovers a surprise.

ivp = ode;
ivp.ODEFcn = @(t, u, p) u^2 - u^3;
ivp.InitialValue = 0.005;

We will solve the problem first with the implicit AM2 method using n=200n=200 steps.

[tI, uI] = am2(ivp, 0, 400, 200);
clf
plot(tI, uI)
xlabel("t");  ylabel(("u(t)"));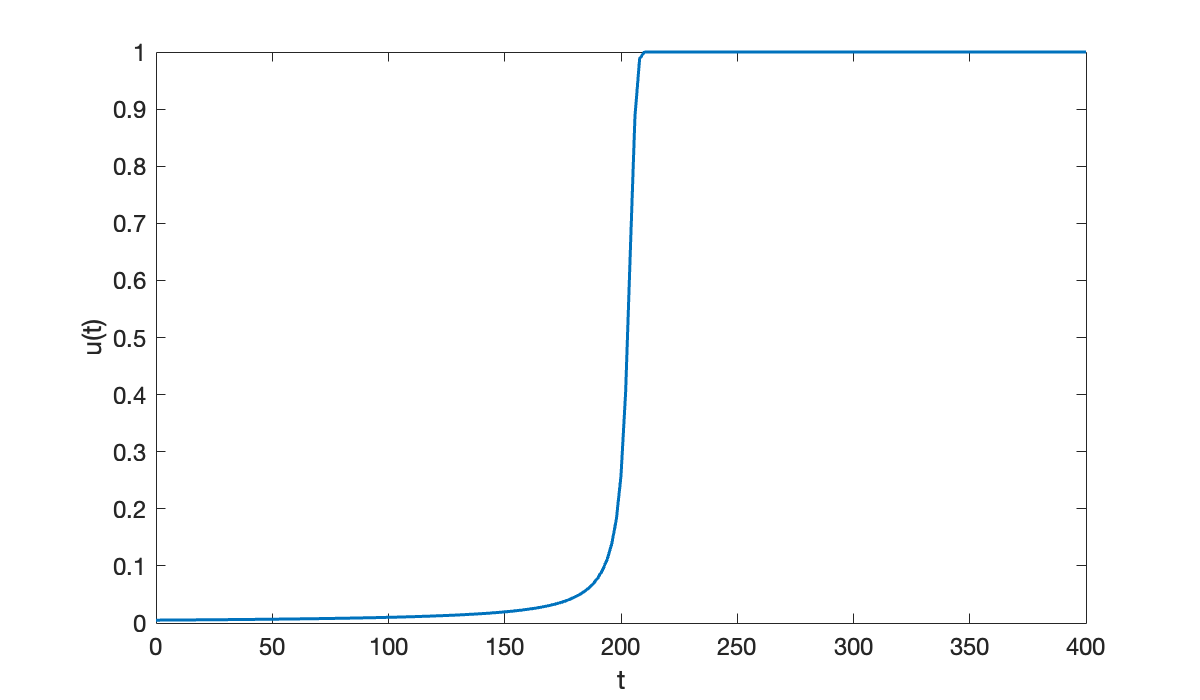
Image produced in Jupyter

Now we repeat the process using the explicit AB4 method.

[tE, uE] = ab4(ivp, 0, 400, 200);
hold on
plot(tE, uE, '.', 'markersize', 8)
ylim([-5, 3])
legend("AM2", "AB4");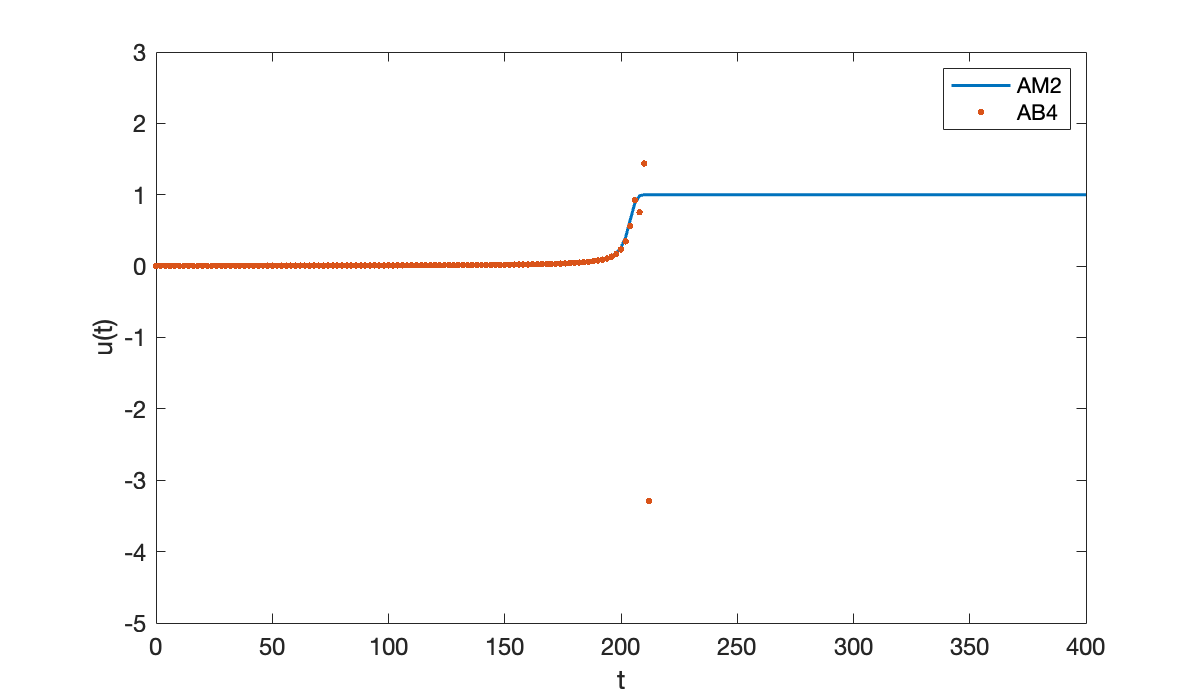
Image produced in Jupyter

Once the solution starts to take off, the AB4 result goes catastrophically wrong.

format short e
uE(105:111)
Loading...

We hope that AB4 will converge in the limit h→0h\to 0, so let’s try using more steps.

clf,  plot(tI, uI, '.', 'markersize', 10)
hold on
[tE, uE] = ab4(ivp, 0, 400, 1000);
plot(tE, uE)
[tE, uE] = ab4(ivp, 0, 400, 1600);
plot(tE, uE)
legend("AM2, n=200", "AB4, n=1000", "AB4, n=1600", location="northwest");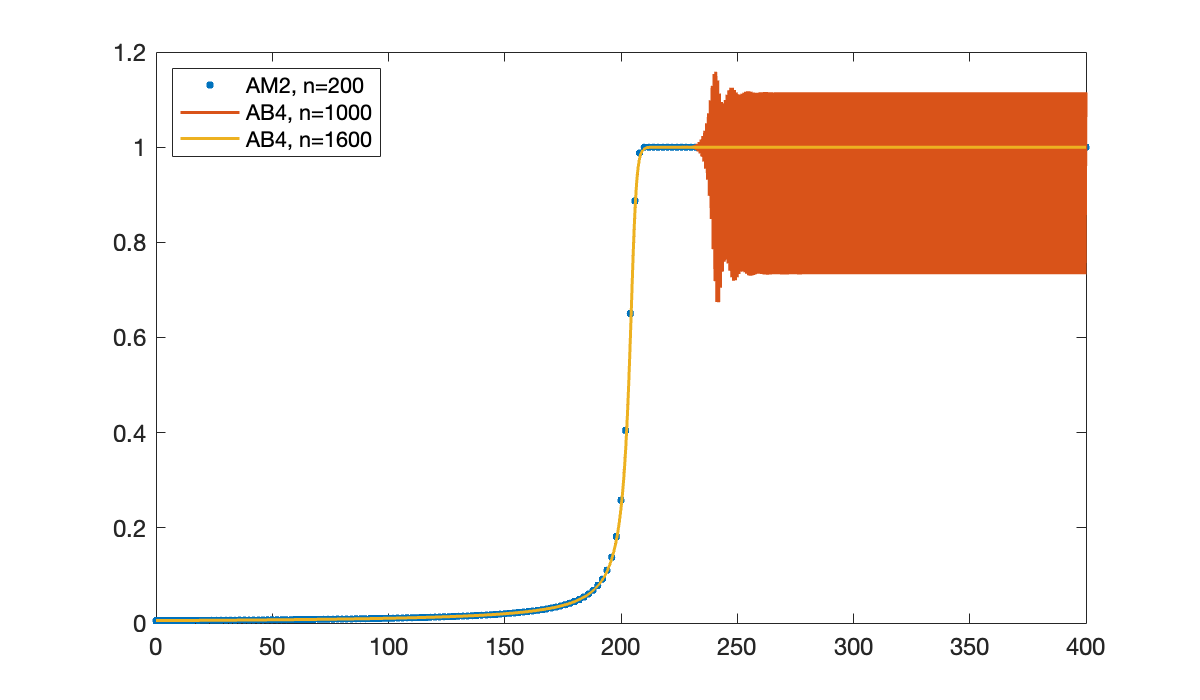
Image produced in Jupyter

So AB4, which is supposed to be more accurate than AM2, actually needs something like 8 times as many steps to get a reasonable-looking answer!

6.7 Implementation of multistep methods

Example 6.8.1

We’ll measure the error at the time t=1t=1.

du_dt = @(t, u) u;
u_exact = @exp;
a = 0;  b = 1;
n = [5, 10, 20, 40, 60]';
err = zeros(size(n));
for j = 1:length(n)
    h = (b - a) / n(j);
    t = a + h *(0:n(j));
    u = [1, u_exact(h), zeros(1, n(j) - 1)];
    f = [du_dt(t(1), u(1)), zeros(1, n(j) - 2)];
    for i = 2:n(j)
        f(i) = du_dt(t(i), u(i));
        u(i+1) = -4*u(i) + 5*u(i-1) + h * (4*f(i) + 2*f(i-1));
    end
    err(j) = abs(u_exact(b) - u(end));
end

h = (b-a) ./ n;
disp(table(n, h, err))
        n             h            err    

    __________    __________    __________


    5.0000e+00    2.0000e-01    1.6045e-02

    1.0000e+01    1.0000e-01    2.8455e+00

    2.0000e+01    5.0000e-02    1.6225e+06

    4.0000e+01    2.5000e-02    9.3442e+18

    6.0000e+01    1.6667e-02    1.7401e+32

The error starts out promisingly, but things explode from there. A graph of the last numerical attempt yields a clue.

clf
semilogy(t, abs(u))
xlabel("t");  ylabel("|u(t)|")
title(("LIAF solution"));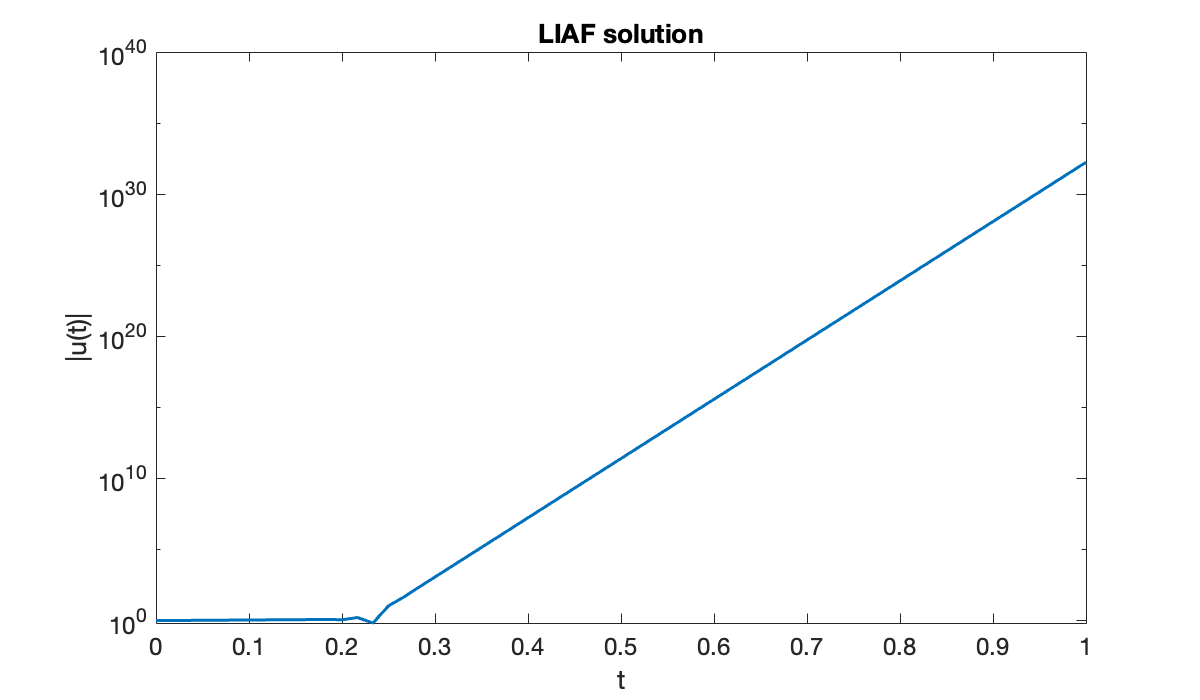
Image produced in Jupyter

It’s clear that the solution is growing exponentially in time.

MATLAB codes
Chapter 5
MATLAB codes
Chapter 7