Functions¶
Euler’s method for an initial-value problem
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16def euler(du_dt, tspan, u0, n): """ euler(du_dt, tspan, u0, n) Apply Euler's method to solve the IVP u'=du_dt(u,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. Return vectors of times and solution values. """ a, b = tspan h = (b - a) / n t = np.linspace(a, b, n+1) u = np.tile(np.array(u0), (n+1, 1)) for i in range(n): u[i+1] = u[i] + h * du_dt(t[i], u[i]) return t, u.T
Improved Euler method for an IVP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22def ie2(du_dt, tspan, u0, n): """ ie2(du_dt, tspan, u0, n) Apply the Improved Euler method to solve the vector-valued IVP u'=du_dt(u,p,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. Returns a vector of times and a vector of solution values/vectors. """ # Time discretization. a, b = tspan h = (b - a) / n t = np.linspace(a, b, n + 1) # Initialize output. u = np.tile(np.array(u0), (n+1, 1)) # Time stepping. for i in range(n): uhalf = u[i] + h / 2 * du_dt(t[i], u[i]) u[i+1] = u[i] + h * du_dt(t[i] + h / 2, uhalf) return t, u.T
Fourth-order Runge-Kutta for an IVP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25def rk4(du_dt, tspan, u0, n): """ rk4(du_dt, tspan, u0, n) Apply "the" Runge-Kutta 4th order method to solve the vector-valued IVP u'=du_dt(u,p,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. Return a vector of times and a vector of solution values/vectors. """ # Time discretization. a, b = tspan h = (b - a) / n t = np.linspace(a, b, n + 1) # Initialize output. u = np.tile(np.array(u0), (n+1, 1)) # Time stepping. for i in range(n): k1 = h * du_dt(t[i], u[i]) k2 = h * du_dt(t[i] + h / 2, u[i] + k1 / 2) k3 = h * du_dt(t[i] + h / 2, u[i] + k2 / 2) k4 = h * du_dt(t[i] + h, u[i] + k3) u[i+1] = u[i] + (k1 + 2 * (k2 + k3) + k4) / 6 return t, u.T
Adaptive IVP solver based on embedded RK formulas
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16def euler(du_dt, tspan, u0, n): """ euler(du_dt, tspan, u0, n) Apply Euler's method to solve the IVP u'=du_dt(u,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. Return vectors of times and solution values. """ a, b = tspan h = (b - a) / n t = np.linspace(a, b, n+1) u = np.tile(np.array(u0), (n+1, 1)) for i in range(n): u[i+1] = u[i] + h * du_dt(t[i], u[i]) return t, u.T
About the code
The check t[i]+h==t[i]on line 19 is to detect when has become so small that it no longer changes the floating-point value of . This may be a sign that the underlying exact solution has a singularity near , but in any case, the solver must halt by using a break statement to exit the loop.
On line 30, we use a combination of absolute and relative tolerances to judge the acceptability of a solution value, as in (5.7.6). In lines 41--43 we underestimate the step factor a bit and prevent a huge increase in the step size, since a rejected step is expensive, and then we make sure that our final step doesn’t take us past the end of the domain.
Finally, line 37 exploits a subtle property of the BS23 formula called first same as last (FSAL).
While (6.5.5) calls for four stages to find the paired second- and third-order estimates, the final stage computed in stepping from to is identical to the first stage needed to step from to . By repurposing s₄ as s₁ for the next pass, one of the stage evaluations comes for free, and only three evaluations of are needed per successful step.
4th-order Adams–Bashforth formula for an IVP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30def ab4(du_dt, tspan, u0, n): """ ab4(du_dt, tspan, u0, n) Apply the Adams-Bashforth 4th order method to solve the vector-valued IVP u'=du_dt(u,p,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. """ # Time discretization. a, b = tspan h = (b - a) / n t = np.linspace(a, b, n + 1) # Constants in the AB4 method. k = 4 sigma = np.array([55, -59, 37, -9]) / 24 # Find starting values by RK4. ts, us = rk4(du_dt, [a, a + (k - 1) * h], u0, k - 1) u = np.tile(np.array(u0), (n+1, 1)) u[:k] = us[:k].T # Compute history of u' values, from newest to oldest. f = np.array([du_dt(t[k-j-2], u[k-j-2]) for j in range(k)]) # Time stepping. for i in range(k-1, n): f = np.vstack([du_dt(t[i], u[i]), f[:-1]]) # new value of du/dt u[i+1] = u[i] + h * np.dot(sigma, f) # advance one step return t, u.T
About the code
Line 15 sets σ to be the coefficients of the generating polynomial of AB4. Lines 19--21 set up the IVP over the time interval , call rk4 to solve it using the step size , and use the result to fill the first four values of the solution. Then line 24 computes the vector .
Line 28 computes , based on the most recent solution value and time. That goes into the first spot of f, followed by the three values that were previously most recent. These are the four values that appear in (6.7.1). Each particular value starts at the front of f, moves through each position in the vector over three iterations, and then is forgotten.
2nd-order Adams–Moulton (trapezoid) formula for an IVP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25def am2(du_dt, tspan, u0, n): """ am2(du_dt, tspan, u0, n) Apply the Adams-Moulton 2nd order method to solve the vector-valued IVP u'=du_dt(u,p,t) over the interval tspan with u(tspan[1])=u0, using n subintervals/steps. """ # Time discretization. a, b = tspan h = (b - a) / n t = np.linspace(a, b, n + 1) # Initialize output. u = np.tile(np.array(u0), (n+1, 1)) # Time stepping. for i in range(n): # Data that does not depend on the new value. known = u[i] + h / 2 * du_dt(t[i], u[i]) # Find a root for the new value. F = lambda z: z - h / 2 * du_dt(t[i+1], z) - known unew = levenberg(F, known) u[i+1] = unew[-1] return t, u.T
About the code
Lines 22-23 define the function and call levenberg to find the new solution value, using an Euler half-step as its starting value. A robust code would have to intercept the case where levenberg fails to converge, but we have ignored this issue for the sake of brevity.
Examples¶
6.1 Basics of IVPs¶
Example 6.1.2
Let’s use solve_ivp from scipy.integrate to define and solve an initial-value problem for over , such that .
To create an initial-value problem for , you must supply a function that computes , an initial value for , and the endpoints of the interval for . The interval should be defined as (a,b), where at least one of the values is a float.
f = lambda t, u: sin((t + u) ** 2)
tspan = [0.0, 4.0]
u0 = [-1.0]Note above that even though this is a problem for a scalar function , we had to set the initial condition as a “one-dimensional vector.”
from scipy.integrate import solve_ivp
sol = solve_ivp(f, tspan, u0)The resulting solution object has fields t and y that contain the values of the independent and dependent variables, respectively; those field names are the same regardless of what we use in our own codes.
print("t shape:", sol.t.shape)
print("u shape:", sol.y.shape)
plot(sol.t, sol.y[0, :], "-o")
xlabel("$t$"), ylabel("$u(t)$")
title(("Solution of $u' = sin((t+u)^2)$"));t shape: (10,)
u shape: (1, 10)
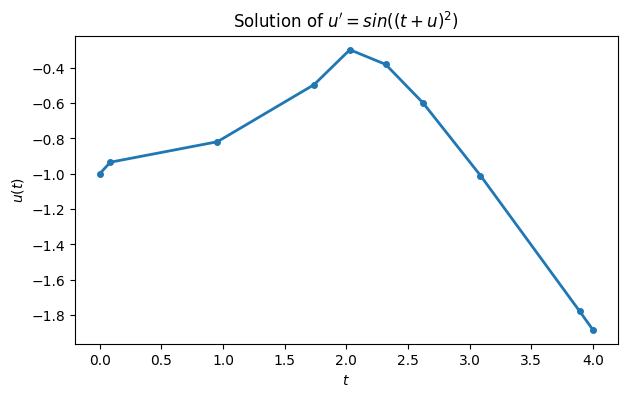
You can see above that the solution was not computed at enough points to make a smooth graph. There is a way to request output at times of your choosing.
sol = solve_ivp(f, tspan, u0, t_eval=linspace(0, 4, 200))
plot(sol.t, sol.y[0, :], "-")
xlabel("$t$"), ylabel("$u(t)$")
title(("Solution of $u' = sin((t+u)^2)$"));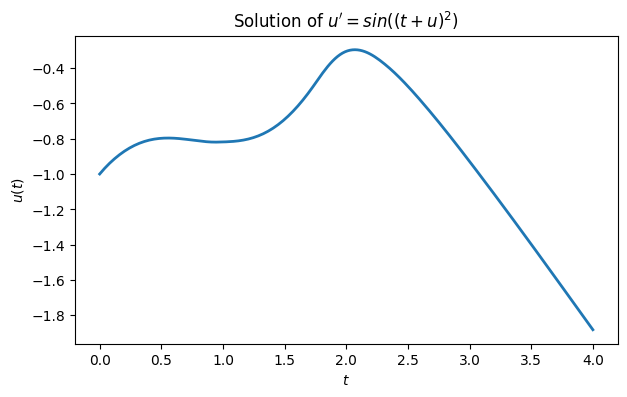
Another option is to enable interpolation to evaluate the solution anywhere after the fact:
sol = solve_ivp(f, tspan, u0, dense_output=True)
for t in linspace(0, 4, 6):
print(f"u({t:.2f}) = {sol.sol(t)[0]:.4f}")u(0.00) = -1.0000
u(0.80) = -0.8122
u(1.60) = -0.6204
u(2.40) = -0.4320
u(3.20) = -1.1139
u(4.00) = -1.8822
Example 6.1.3
The equation gives us some trouble.
Tip
It’s a good idea to check sol.success after calling solve_ivp. If it’s False, the solution may not be reliable.
f = lambda t, u: (t + u) ** 2
sol = solve_ivp(f, [0.0, 1.0], [1.0])
if not sol.success:
print(sol.message)Required step size is less than spacing between numbers.
The warning message we received can mean that there is a bug in the formulation of the problem. But if everything has been done correctly, it suggests that the solution may not exist past the indicated time. This is a possibility in nonlinear ODEs.
semilogy(sol.t, sol.y[0, :])
xlabel("$t$")
ylabel("$u(t)$")
title(("Blowup in finite time"));
Example 6.1.5
Consider the ODEs and . In each case we compute , so the condition number bound from Theorem 6.1.2 is in both problems. However, they behave quite differently. In the case of exponential growth, , the bound is the actual condition number.
t = linspace(0, 3, 200)
u = array([exp(t) * u0 for u0 in [0.7, 1, 1.3]])
plot(t, u.T)
xlabel("$t$")
ylabel("$u(t)$")
title(("Exponential divergence of solutions"));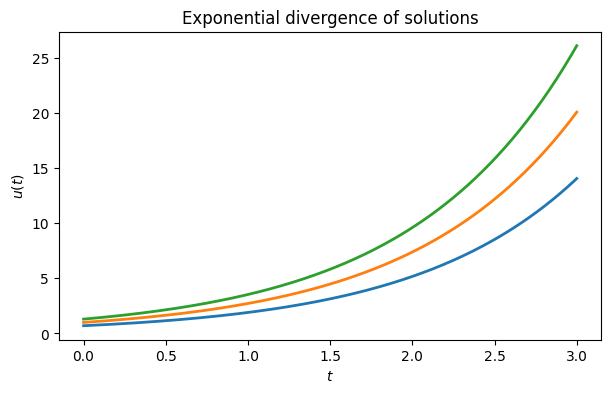
But with , solutions actually get closer together with time.
t = linspace(0, 3, 200)
u = array([exp(-t) * u0 for u0 in [0.7, 1, 1.3]])
plot(t, u.T)
xlabel("$t$")
ylabel("$u(t)$")
title(("Exponential convergence of solutions"));
In this case the actual condition number is one, because the initial difference between solutions is the largest over all time. Hence, the exponentially growing upper bound is a gross overestimate.
6.2 Euler’s method¶
Example 6.2.1
We consider the IVP over , with .
f = lambda t, u: sin((t + u) ** 2)
tspan = [0.0, 4.0]
u0 = -1.0
t, u = FNC.euler(f, tspan, u0, 20)
fig, ax = subplots()
ax.plot(t, u[0, :], "-o", label="$n=20$")
xlabel("$t$"), ylabel("$u(t)$")
title("Solution by Euler's method")
legend();
We could define a different interpolant to get a smoother picture above, but the derivation of Euler’s method assumed a piecewise linear interpolant. We can instead request more steps to make the interpolant look smoother.
t, u = FNC.euler(f, tspan, u0, 200)
ax.plot(t, u[0, :], label="$n=200$")
ax.legend()
fig
Increasing changed the solution noticeably. Since we know that interpolants and finite differences become more accurate as , we should anticipate the same behavior from Euler’s method. We don’t have an exact solution to compare to, so we will use solve_ivp to construct an accurate reference solution.
from scipy.integrate import solve_ivp
sol = solve_ivp(f, tspan, [u0], dense_output=True, atol=1e-8, rtol=1e-8)
ax.plot(t, sol.sol(t)[0, :], "--", label="accurate")
ax.legend()
fig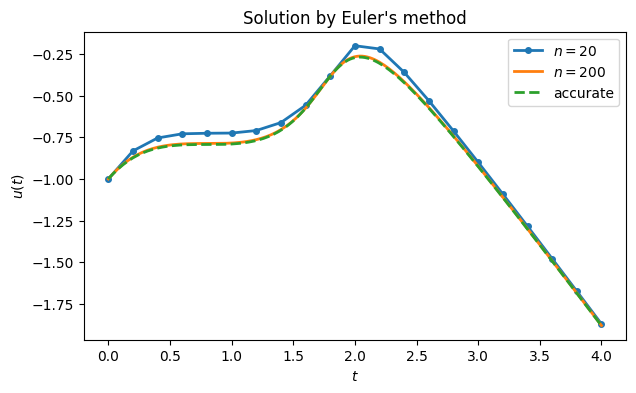
Now we can perform a convergence study.
n_ = array([int(5 * 10**k) for k in arange(0, 3, 0.5)])
err_ = zeros(6)
results = PrettyTable(["n", "error"])
for j, n in enumerate(n_):
t, u = FNC.euler(f, tspan, u0, n)
err_[j] = norm(sol.sol(t)[0, :] - u[0, :], inf)
results.add_row((n, err_[j]))
print(results)+------+-----------------------+
| n | error |
+------+-----------------------+
| 5 | 2.734204988403654 |
| 15 | 0.15019897709240698 |
| 50 | 0.02999619702005879 |
| 158 | 0.008850284724318591 |
| 500 | 0.0027366205261468157 |
| 1581 | 0.0008596857693601301 |
+------+-----------------------+
The error is approximately cut by a factor of 10 for each increase in by the same factor. A log-log plot also confirms first-order convergence. Keep in mind that since , it follows that .
loglog(n_, err_, "-o", label="results")
plot(n_, 0.5 * (n_ / n_[0])**(-1), "--", label="1st order")
xlabel("$n$"), ylabel("inf-norm error")
title("Convergence of Euler's method")
legend();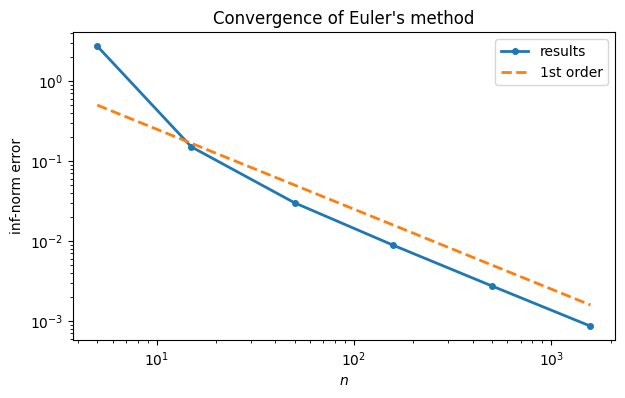
6.3 IVP systems¶
Example 6.3.2
We encode the predator–prey equations via a function.
def predprey(t, u):
y, z = u # rename for convenience
s = (y * z) / (1 + beta * y) # appears in both equations
return array([y * (1 - alpha * y) - s, -z + s])As before, the ODE function must accept three inputs, u, p, and t, even though in this case there is no explicit dependence on t. The second input is used to pass parameters that don’t change throughout a single instance of the problem.
To specify the IVP we must also provide the initial condition, which is a 2-vector here, and the interval for the independent variable. These are given in the call to solve_ivp.
from scipy.integrate import solve_ivp
u0 = array([1, 0.01])
tspan = [0.0, 80.0]
alpha, beta = 0.1, 0.25
sol = solve_ivp(predprey, tspan, u0, dense_output=True)
print(f"solved with {sol.y.shape[1]} time steps")solved with 102 time steps
As in scalar problems, the solution object has fields t and y that contain the values of the independent and dependent variables, respectively. Each row of y represents one component of the solution at every time step, and each column of y is the entire solution vector at one time step. Since we used dense_output=True, there is also a method sol that can be used to evaluate the solution at any time.
t = linspace(0, 80, 1200)
u = vstack([sol.sol(t[i]) for i in range(t.size)]).T # same shape as sol.y
fig, ax = subplots()
ax.plot(t, u[0, :], label="prey")
ax.plot(t, u[1, :], label="predator")
xlabel("$t$"), ylabel("population")
title(("Predator-prey solution"));
We can also use Function 6.2.2 to find the solution.
t_E, u_E = FNC.euler(predprey, tspan, u0, 800)
ax.scatter(t_E, u_E[0, :], label="prey (Euler)", s=1)
ax.scatter(t_E, u_E[1, :], label="predator (Euler)", s=2)
ax.legend()
fig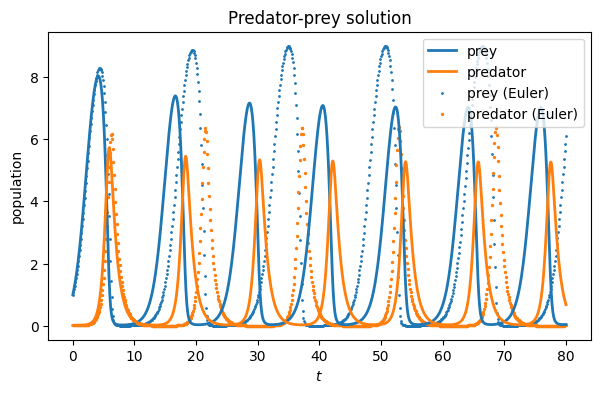
You can see above that the Euler solution is not very accurate. When the solution has two components, it’s common to plot the it in the phase plane, i.e., with and along the axes and time as a parameterization of the curve.
plot(u[0, :], u[1, :])
xlabel("prey"), ylabel("predator")
title(("Predator-prey phase plane"));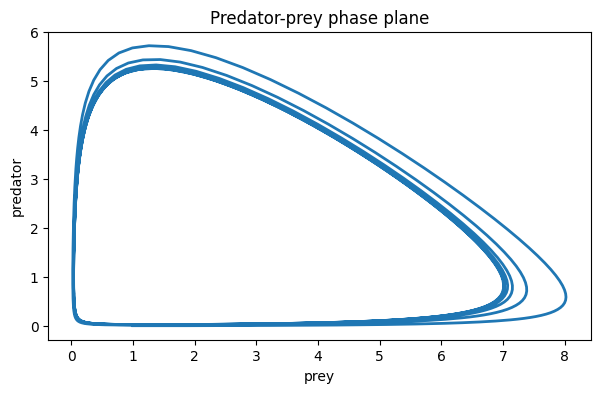
From this plot we can see that the solution approaches a periodic one, which in the phase plane is represented by a closed path.
Example 6.3.5
Let’s implement the coupled pendulums from Example 6.3.4. The pendulums will be pulled in opposite directions and then released together from rest.
def couple(t, u, params):
gamma, L, k = params
g = 9.8
udot = copy(u)
udot[:2] = u[2:4]
udot[2] = -gamma * u[2] - (g / L) * sin(u[0]) + k * (u[1] - u[0])
udot[3] = -gamma * u[3] - (g / L) * sin(u[1]) + k * (u[0] - u[1])
return udot
u0 = array([1.25, -0.5, 0, 0])
tspan = [0.0, 50.0]First we check the behavior of the system when the pendulums are uncoupled, i.e., when .
Tip
We use a closure here to pass the fixed parameter values into couple.
gamma, L, k = 0.01, 0.5, 0.0
du_dt = lambda t, u: couple(t, u, (gamma, L, k))
sol = solve_ivp(du_dt, tspan, u0, t_eval=linspace(0, 50, 1000))
plot(sol.t, sol.y[:2, :].T) # first two components of solution
xlabel("t"), ylabel("angle")
title("Uncoupled pendulums");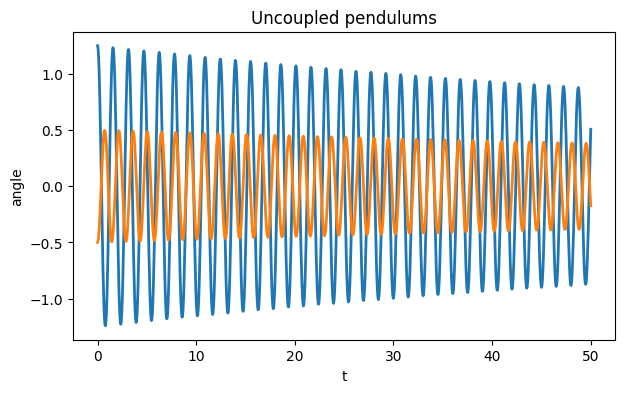
You can see that the pendulums swing independently. Because the model is nonlinear and the initial angles are not small, they have slightly different periods of oscillation, and they go in and out of phase.
With coupling activated, a different behavior is seen.
k = 0.75 # changes the value in the du_dt closure
sol = solve_ivp(du_dt, tspan, u0, t_eval=linspace(0, 50, 1000))
plot(sol.t, sol.y[:2, :].T)
xlabel("t"), ylabel("angle")
title("Coupled pendulums");
The coupling makes the pendulums swap energy back and forth.
6.4 Runge–Kutta methods¶
Example 6.4.1
We solve the IVP over , with . We start by getting a reference solution to validate against.
from scipy.integrate import solve_ivp
du_dt = lambda t, u: sin((t + u)**2)
tspan = (0.0, 4.0)
u0 = -1.0
sol = solve_ivp(du_dt, tspan, [u0], dense_output=True, atol=1e-13, rtol=1e-13)
u_ref = sol.solNow we perform a convergence study of our two Runge–Kutta implementations.
n = array([int(2 * 10**k) for k in linspace(0, 3, 7)])
err = {"IE2" : [], "RK4" : []}
results = PrettyTable(["n", "IE2 error", "RK4 error"])
for i in range(len(n)):
t, u = FNC.ie2(du_dt, tspan, u0, n[i])
err["IE2"].append( abs(u_ref(4)[0] - u[0][-1]) )
t, u = FNC.rk4(du_dt, tspan, u0, n[i])
err["RK4"].append( abs(u_ref(4)[0] - u[0][-1]) )
results.add_row([n[i], err["IE2"][-1], err["RK4"][-1]])
print(results)+------+------------------------+------------------------+
| n | IE2 error | RK4 error |
+------+------------------------+------------------------+
| 2 | 1.7690264118810441 | 0.8206513302232612 |
| 6 | 0.5126838225133257 | 0.7919245473433536 |
| 20 | 0.002966971266360252 | 4.0177650143746746e-05 |
| 63 | 0.00021416270501584123 | 3.581705267929891e-07 |
| 200 | 1.951309601522233e-05 | 3.326041442264227e-09 |
| 632 | 1.9058382192405077e-06 | 3.2657876403163755e-11 |
| 2000 | 1.8883901087285437e-07 | 2.6711965972481266e-13 |
+------+------------------------+------------------------+
The amount of computational work at each time step is assumed to be proportional to the number of stages. Let’s compare on an apples-to-apples basis by using the number of -evaluations on the horizontal axis.
loglog(2 * n, err["IE2"], "-o", label="IE2")
loglog(4 * n, err["RK4"], "-o", label="RK4")
plot(2 * n, 0.5 * err["IE2"][-1] * (n / n[-1])**(-2), "--", label="2nd order")
plot(4 * n, 0.5 * err["RK4"][-1] * (n / n[-1])**(-4), "--", label="4th order")
xlabel("f-evaluations"), ylabel("inf-norm error")
legend()
title("Convergence of RK methods");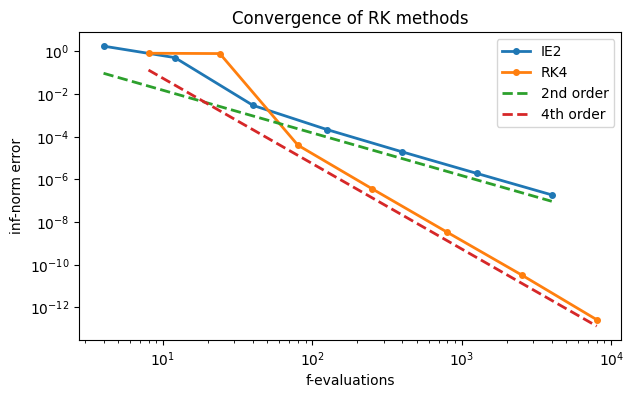
The fourth-order variant is more efficient in this problem over a wide range of accuracy.
6.5 Adaptive Runge–Kutta¶
Example 6.5.1
Let’s run adaptive RK on .
f = lambda t, u: exp(t - u * sin(u))
t, u = FNC.rk23(f, [0.0, 5.0], [0.0], 1e-5)
scatter(t, u[0, :])
xlabel("$t$"), ylabel("$u(t)$")
title(("Adaptive IVP solution"));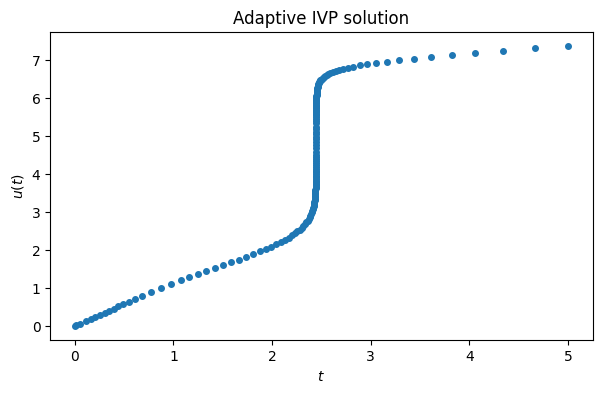
The solution makes a very abrupt change near . The resulting time steps vary over three orders of magnitude.
dt = [t[i + 1] - t[i] for i in range(t.size - 1)]
semilogy(t[:-1], dt)
xlabel("$t$"), ylabel("time step")
title(("Adaptive step sizes"));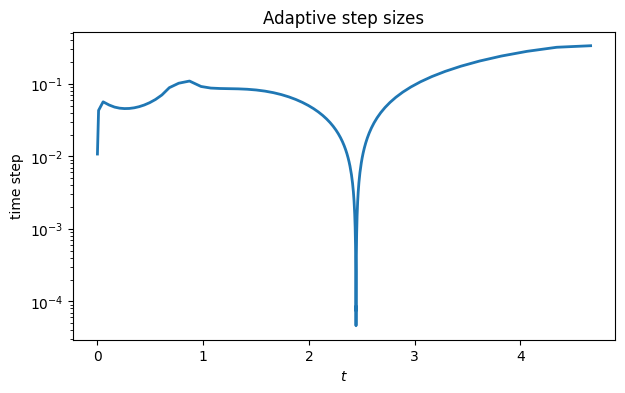
If we had to run with a uniform step size to get this accuracy, it would be
print(f"min step size was {min(dt):.2e}")min step size was 4.61e-05
On the other hand, the average step size that was actually taken was
print(f"mean step size was {mean(dt):.2e}")mean step size was 3.21e-02
We took fewer steps by a factor of 1000! Even accounting for the extra stage per step and the occasional rejected step, the savings are clear.
Example 6.5.2
In Demo 6.1.3 we saw an IVP that appears to blow up in a finite amount of time. Because the solution increases so rapidly as it approaches the blowup, adaptive stepping is required even to get close.
du_dt = lambda t, u: (t + u)**2
tspan = (0.0, 2.0)
u0 = [1.0]
t, u = FNC.rk23(du_dt, tspan, u0, 1e-5)/Users/driscoll/Dropbox/Mac/Documents/GitHub/fnc/python/fncbook/fncbook/chapter06.py:90: UserWarning: Stepsize too small near t=0.785408720407281
warnings.warn(f"Stepsize too small near t={t[i]}")
In fact, the failure of the adaptivity gives a decent idea of when the singularity occurs.
semilogy(t, u[0, :])
xlabel("$t$"), ylabel("$u(t)$")
title("Finite-time blowup")
tf = t[-1]
axvline(x=tf, color='k', linestyle='--', label=f"t = {tf:.6f}")
legend();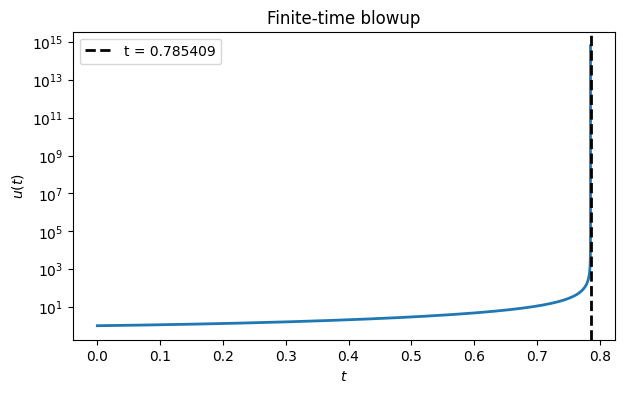
6.6 Multistep methods¶
Example 6.7.1
We study the convergence of AB4 using the IVP over , with . As usual, solve_ivp is called to give an accurate reference solution.
from scipy.integrate import solve_ivp
du_dt = lambda t, u: sin((t + u)**2)
tspan = (0.0, 4.0)
u0 = [-1.0]
u_ref = solve_ivp(du_dt, tspan, u0, dense_output=True, rtol=1e-13, atol=1e-13).solNow we perform a convergence study of the AB4 code.
n = array([int(4 * 10**k) for k in linspace(0, 3, 7)])
err = []
results = PrettyTable(["n", "AB4 error"])
for i in range(len(n)):
t, u = FNC.ab4(du_dt, tspan, u0, n[i])
err.append( abs(u_ref(4)[0] - u[0][-1]) )
results.add_row([n[i], err[-1]])
print(results)+------+------------------------+
| n | AB4 error |
+------+------------------------+
| 4 | 0.5004401704518087 |
| 12 | 0.9739144270683646 |
| 40 | 2.2180676292116175e-05 |
| 126 | 3.9306304588926366e-07 |
| 400 | 4.561844235695389e-09 |
| 1264 | 4.791389507374788e-11 |
| 4000 | 5.426770144367765e-13 |
+------+------------------------+
The method should converge as , so a log-log scale is appropriate for the errors.
loglog(n, err, "-o", label="AB4")
loglog(n, 0.5 * err[-1] * (n / n[-1])**(-4), "--", label="4th order")
xlabel("$n$"), ylabel("final error")
legend(), title("Convergence of AB4");
Example 6.7.2
The following simple ODE uncovers a surprise.
f = lambda t, u: u**2 - u**3
u0 = array([0.005])
tspan = [0, 400]We will solve the problem first with the implicit AM2 method using steps.
tI, uI = FNC.am2(f, [0.0, 400.0], u0, 200)
fig, ax = subplots()
ax.plot(tI, uI[0], label="AM2")
xlabel("$t$"), ylabel("$y(t)$");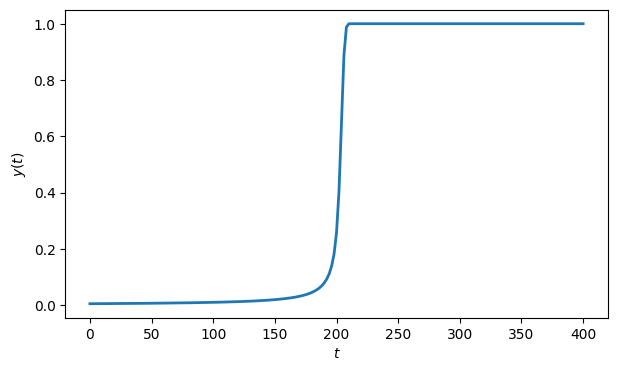
So far, so good. Now we repeat the process using the explicit AB4 method.
tE, uE = FNC.ab4(f, [0.0, 400.0], u0, 200)
ax.scatter(tE, uE[0], label="AB4")
ax.set_ylim([-4, 2]), ax.legend()
fig/var/folders/gc/0752xrm56pnf0r0dsrn5370c0000gr/T/ipykernel_93665/862619530.py:1: RuntimeWarning: overflow encountered in square
f = lambda t, u: u**2 - u**3
/var/folders/gc/0752xrm56pnf0r0dsrn5370c0000gr/T/ipykernel_93665/862619530.py:1: RuntimeWarning: overflow encountered in power
f = lambda t, u: u**2 - u**3
/var/folders/gc/0752xrm56pnf0r0dsrn5370c0000gr/T/ipykernel_93665/862619530.py:1: RuntimeWarning: invalid value encountered in subtract
f = lambda t, u: u**2 - u**3
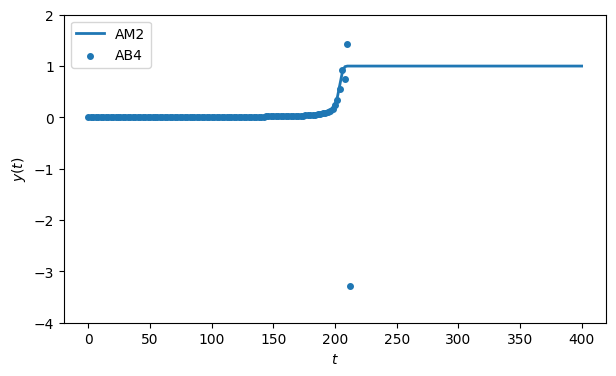
Once the solution starts to take off, the AB4 result goes catastrophically wrong.
uE[0, 104:111]array([ 7.55385780e-01, 1.43729703e+00, -3.28897685e+00, 2.14179113e+02,
-4.48208915e+07, 4.12689029e+23, -3.22144124e+71])We hope that AB4 will converge in the limit , so let’s try using more steps.
plot(tI, uI[0], color="k", label="AM2")
tE, uE = FNC.ab4(f, [0, 400], u0, 1000)
plot(tE, uE[0], ".-", label="AM4, n=1000")
tE, uE = FNC.ab4(f, [0, 400], u0, 1600)
plot(tE, uE[0], ".-", label="AM4, n=1600")
xlabel("$t$"), ylabel("$u(t)$")
legend();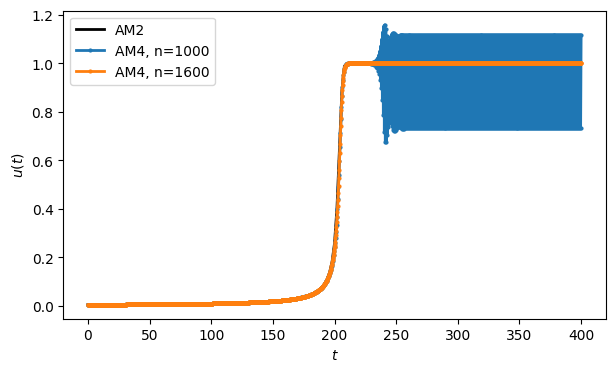
So AB4, which is supposed to be more accurate than AM2, actually needs something like 8 times as many steps to get a reasonable-looking answer!
6.7 Implementation of multistep methods¶
Example 6.8.1
We’ll measure the error at the time .
du_dt = lambda t, u: u
u_exact = exp
a, b = (0.0, 1.0)
def LIAF(du_dt, tspan, u0, n):
a, b = tspan
h = (b - a) / n
t = linspace(a, b, n+1)
u = np.tile(np.array(u0), (n+1, 1))
u[1] = u_exact(t[1]) # use an exact starting value
f = copy(u)
f[0] = du_dt(t[0], u[0])
for i in range(n):
f[i] = du_dt(t[i], u[i])
u[i + 1] = -4 * u[i] + 5 * u[i-1] + h * (4 * f[i] + 2 * f[i-1])
return t, u.T
n = [5, 10, 20, 40, 60]
results = PrettyTable(["n", "error"])
for j in range(5):
t, u = LIAF(du_dt, [a, b], [1.0], n[j])
err = abs(u_exact(b) - u[0, -1])
results.add_row([n[j], err])
print(results)+----+------------------------+
| n | error |
+----+------------------------+
| 5 | 293.502838171541 |
| 10 | 452905.58324991807 |
| 20 | 2196838145485.221 |
| 40 | 1.0437865522698013e+26 |
| 60 | 6.628042953187168e+39 |
+----+------------------------+
There is no convergence in sight! A graph of the last numerical attempt yields a clue:
semilogy(t, abs(u[0]), "-o")
xlabel("$t$"), ylabel("$|u|$")
title(("LIAF solution"));
It’s clear that the solution is growing exponentially in time.